2016年8月の記事

メディカルクオークグループの代表を務める門脇先生が数学と理科の特別授業を行います。

難易度の高い問題も簡単に解りやすく解説してくれます。

授業を通じて効率の良い学習法・解法を身につけていきましょう。

第２４回．特別授業－医学部物理解法（東海大学物理2012年第3問）

【タイトル】
〜熱力学、高速解法〜

「言葉からの反射」で、難関な医学部の問題を教科書の公式だけで反射的に解く

【前説】
今回は、医学部受験の入門大学として人気な東海大学。その中でも、物理を例にとって説明します。

【門脇メソッド】
「言葉からの反射」未修分野でも、閃ける

今回は簡単です。問題数は多いんですが、「言葉からの反射」が公式一発でほぼ終わります。先週の真逆と考えてよいでしょう。

問題数が多い時は、この傾向が強いですね。ガンガン行きましょう！

そうすると・・・

【対象の学力層】
（上級～中級ランクまでしか受けない人は、「終わりに」の前から読んで下さい)

言葉からの反射を使って、医学部の入試問題を教科書に載っている単純な公式まで分解していきます！

今日から、医学部レベルの学力を「分単位！！」で身に着けていきましょう。

【物理の対策】
「言葉からの反射」に入る前に、今回は、物理の対策について説明しますね！ 今日は物理なので、

知識、知識の関連性	最少、多い
論理展開	中

と言えます。

こういう科目は、「言葉からの反射」が全てです。東海大学なら、平易な公式集か、そもそも教科書の裏表紙で十分でしょう。

では、解く＆覚えていきましょう。

レベル１レベル２　では非常に単純化していきましょう＋言葉からの反射表を作っていきましょう。

【問題】
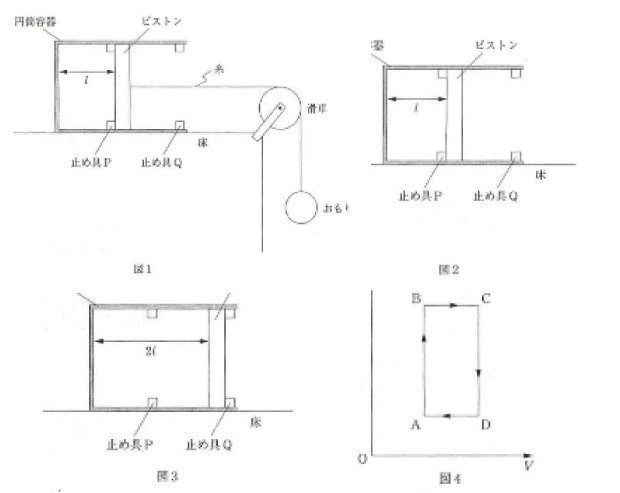
大気中で、床に固定された円筒容器に、なめらかに動く軽いピストンでn［mol］の単原子分子の理想気体を封じた。

このときの気体の圧力は大気圧ｐ0［Pa］に等しかった。次に軽い糸をピストンに取り付け、糸の一方の端を滑らかに回る滑車に通し、糸が床に平行となるように保った状態で質量ｍ［kg］のおもりをぶら下げた。その結果図１のように、ピストンは円筒容器の底からｌ［ｍ］の位置を静止した。

その後、小さな体積の無視できる止め具Ｐをピストンに接する位置で円筒容器内部に固定し、糸を切り離したところ、図２のように、ピストンは止め具Ｐに接して静止していた。

このときの気体の状態をＡとし、気体の温度をＴ_A［K］とする。

次に、円筒容器に封じた気体をゆっくりと加熱し始めたところ、気体の温度がT_B［K］のときにピストンは止め具Pに接して静止していた。この動き始めたときの気体の状態をBとする。

さらに期待をゆっくりと加熱し続けたところ、図３に示すようにピストンが円筒容器内部に固定された止め具Qに接触して停止した。

接触したときの気体の状態をCとする。状態Cのとき、ピストンは円筒容器の底から２ｌ［ｍ］の位置にあり、気体の温度はT_C［K］であった。

ピストンが止め具Qに接した状態で、再び同じおもりをピストンに糸でつなぎ、気体をゆっくりと冷却した。

しばらくすると気体の温度がT_D［K］となり、ピストンが左へ動き始めた。動き始めたときの気体の状態をDとする。

さらに期待をゆっくりと冷却したところ、気体の状態はAに戻った。

図４は、気体が上記の循環過程A➡B➡C➡D➡Aをたどる間の気体の圧力ｐ［Pa］と体積V［㎥］の関係を示している。

円筒容器の内部の断面積をS［㎡］、気体定数をR［ｊ/（mol・ｋ）］、重力加速の大きさをｇ［ｍ/s²］とし、以下の各問に答えなさい。答えは各問の解答群の中から最も適切なものを一つ選び、解答欄の記号にマークしなさい。

（１） 温度Ｔ_Aを求めなさい。

（２） 温度T_Bを求めなさい。

（３） 温度T_Cを求めなさい。

（４） 温度T_Dを求めなさい。

（５） 気体の状態がBからCに移る過程において円筒容器内の気体がした仕事を求めなさい。

（６） 気体の状態がDからAに移る過程において円筒容器内の気体がした仕事を求めなさい。

（７） 循環過程A➡B➡C➡D➡Aの熱効率を求めなさい。

【解答群】

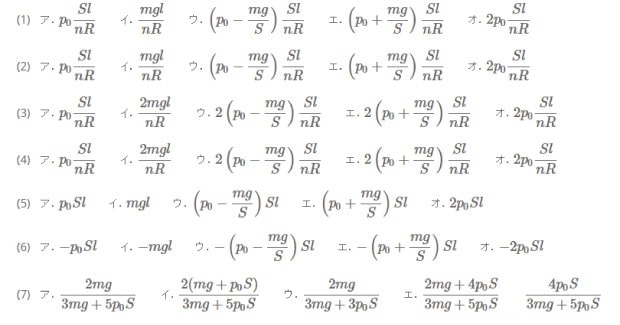
なお、今回は問題数が多いので一瞬驚きます。しかし・・・ジャンルは熱力学の問題です。「～変化」は沢山のパターンが有りますが、基本の解き方は同じです。

（1）
温度＝？
PV=nRT
P＝F/S
F:力の釣り合い(∵「静止していた」)
：F右：おもり、内圧
：F左：外圧（大気圧）
代入して計算すると、

（2）
温度＝？
PV=nRT
代入して計算すると、

（3）
温度＝？
PV=nRT
代入して計算すると、

（4）
温度＝？
PV=nRT
代入して計算すると、

（5）
仕事＝？
W=P⊿V
代入して計算すると、
（＆コラム参照）

（6）
仕事＝？
W=P⊿V
代入して計算すると、
（＆コラム参照）

（7）
熱効率＝？
熱効率＝Qout/Qin
Qout：W（B～C、C～D）（∵A～B,C～Dは⊿V＝０　＠図４）
Qin：　Q（A～B,C～D）（∵B～C、C～DはQ：減少　＠図４）
代入して計算すると、
（＆コラム参照）

答えとしては、
ウ
ア
オ
ウ
ア
ウ

ア

となる。

こんなにシンプルに出来ちゃいます。
普段から解説を読んだり予備校で聞いたりしてると思います。

それは行き当たりばったりの解法であることが多いので、より合理的な手順を教師にも問うようにして下さい。

それでもダメなら、私に質問を送ってくださいね！

帝京大学以上しか受けない人等のこの問題を簡単だと思った人は、今あなたがやっているレベルをこのように解いてみてください。

きっとルールが見えてきて、今あなたがやっている問題でつまずくことが無くなるはずです。

「参考書の解法はルールがない！なんでこの問題だけ変な解き方をするの？」といった意見をよく聞きます。

決してこねくりまわすことなく、書きすぎることなく、かといって止まることもなく、「言葉からの反射」「図からの反射」で簡潔に考える修正をつけましょう。

話が長くなると、自分が混乱しちゃいますよ？

【コラム】熱力学はグラフで解こう
（５）、（６）、（７）のような問題、苦手な人が多いようです。

ですが、熱力学は、グラフが有れば簡単なのです。

W=P⊿V

というのは、Vが変化してなければWは０ということ。

グラフで、Vが変化してないところを探すと、計算が簡単ですね。

熱効率の公式、これは、Qout/Qinと考えましょう

出入り、と考えるわけですね。

すると、QoutはWなので、上のとおり。

Qinは、グラフで、面積が増えているところ。

この問題で言うと、まぁ、図にしましょうか。

C～Dを例に取ると、

Cの時は、赤い部分（紫も含みます）

Dの時は、青い部分（色を混ぜて表現したので、紫の部分）
結果として、赤の部分が残る

つまり、C～Dは減っているということになるわけです。

そうすると、増えている部分は、A～B,C～Dなので、Qinは、

Q（A～B,C～D）

だけということになるわけです。

そういう時は、簡単な数学を使いましょう。

小学校、中学校の知識を使いましょう。上位国立や慶應を相手にするときは、微積以上の数学を除く高校数学が必要な問題も有りますが、私大医学部にはそこまでは必要ありません。

義務教育か一流高校受験レベルの数学でほぼ十分です。

【終わりに】
医学部の物理ですら、九九しかできない人が１ヶ月位で勉強を終えてしまうことが可能です。数学すら簡単な東海大学なので、物理は本当に簡単です。今後も、効率よく勉強して、はやくお医者さんになりましょう！

「言葉からの反射」を使って、出来る限りシンプルに考える習慣を付けましょう！

勉強のやる気が無くなってしまう大きな原因に「飽きる」があります。

反射的に処理して、表にして、1分間でどんどんまとめていく習慣をつけましょう。理解速度が上がりすぎて、勉強せずにはいられなくなりますよ！！　＾O＾

より詳しい説明がほしい方は、いつでもコメント下さい！また、解説して欲しい問題も、募集しています。

第２５回．特別授業－医学部物理解法（東海大学物理2012年第4問）

【タイトル】
〜読解力と図の活用って難しいですか？〜

たった１つの解き方を覚えるだけで、

① 全科目解ける！

② ４倍速で成績が伸びる！

③ 中３から１年で医学部に受かる！

驚異の門脇メソッドとは！？

「言葉からの反射」で、難関な医学部の問題を教科書の公式だけで反射的に解く

【前説】
今回は、医学部受験の入門大学として人気な東海大学。その中でも、物理を例にとって説明します。

【門脇メソッド】
「言葉からの反射」未修分野でも、閃ける

今回は難しいです。問題数も多く、しかも、公式一発では終わりません。「言葉からの反射」、こう言うときにその真価を発揮します！

言葉を全て、反射的に処理してくださいね？

そうすると・・・

【対象の学力層】
今日は、読んだ方が良いです！

（上級～中級ランクまでしか受けない人は、「終わりに」の前から読んで下さい)

言葉からの反射を使って、医学部の入試問題を教科書に載っている単純な公式まで分解していきます！

今日から、医学部レベルの学力を「分単位！！」で身に着けていきましょう。

【物理の対策】
「言葉からの反射」に入る前に、今回は、物理の対策について説明しますね！ 今日は物理なので、

知識、知識の関連性	最少、多い
論理展開	中

と言えます。

こういう科目は、「言葉からの反射」が全てです。東海大学なら、平易な公式集か、そもそも教科書の裏表紙で十分でしょう。

では、解く＆覚えていきましょう。

レベル１レベル２　では非常に単純化していきましょう＋言葉からの反射表を作っていきましょう。

【問題】
図のように、水面上で４ｃｍ離れた2点、A、Bから波長及び振幅がそれぞれ１ｃｍで周期は2秒の波が同位相で出ている。

点Aからの距離が１０ｃｍ、点Bからの距離が８ｃｍの点をPとする。

また、点PからABに平行に引いた直線とABの垂直二等分線の交点をOとする。

以下の各問に答えなさい。答えは各問の解答群の中から最も適切なものを一つ選び、解答欄の記号をマークしなさい。

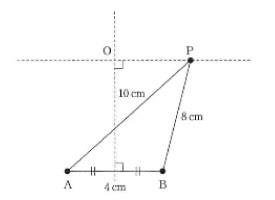
（１） 点Aを出た波が点Pにつくまでにかかる時間は何秒か求めなさい。

（２） 十分に時間が経過後、点Pでの波の振幅の大きさは何ｃｍか求めなさい。点A、Bから出た波が強め合う点、弱め合う点を結んだ線はそれぞれ双曲線となる。

（３） 点Pを通る双曲線はABあるいはABの延長線上のどこで交わるか求めなさい。

（４） 線分PO上で強め合う点はいくつあるか求めなさい。

（５） 点Aから５波長分離れた位置で点Bからの波と強め合う点はいくつあるか求めなさい。

【解答群】

（１）

ア．５　　イ．１０　　ウ．２０　　エ．３０　　オ．４０

（２）

ア．０　　イ．１　　ウ．１．５　　エ．２　　オ．４

（３）

ア．点Aから点Bの方向に１ｃｍのところ
イ．点Aから点Bの方向に２ｃｍのところ
ウ．点Aから点Bの方向に３ｃｍのところ
エ．点Aから点Bの方向に４ｃｍのところ（B点）
オ．点Aから点Bの方向に５ｃｍのところ

（４）

ア．２　　イ．３　　ウ．４　　エ．５　　オ．６

（５）

ア．１　　イ．２　　ウ．４　　エ．８　　オ．１６

なお、今回は問題数が多いので一瞬驚きます。しかし・・・ジャンルは熱力学の問題です。「～変化」は沢山のパターンが有りますが、基本の解き方は同じです。

（1）
かかる時間＝？
ｔ=x/ｖ
ｖ＝ｆλ
ｆ=1/T
代入して計算すると、

（2）※
Pでの振幅＝？
振幅：干渉：強め合いor
λ/2の偶数倍：強め合い
P：A、Bから波が来る、経路差：AP-BP
代入して計算すると、
Pでは強め合うことが分かる
強め合い：振幅の２倍
よって、

（3）※
強め合い・弱め合いの双曲線＝？
図で解く（図が公式にあたる）
双曲線：強め合う点、弱め合う点の図
ある点を通るこの双曲線は、同じ経路差を結ぶ
Pの経路差と同じ、AB上の点は、

（4）※
PO上の強め合う点＝？
P：強め合う
O：強め合う
PとOの間にある、強め合う点は、
λ/2の偶数倍：強め合いなので、
全部の個数は、

（5）※
強め合う点の個数＝？
λ/2の偶数倍になる点の個数
Aから５波長離れた位置：Aを中心とする半径５波長の円上
円と放物線の交点
作図すると、

答えとしては、
ウ
エ
ウ
イ
オ

となる。

こんなにシンプルに出来ちゃいます。
普段から解説を読んだり予備校で聞いたりしてると思います。

それは行き当たりばったりの解法であることが多いので、より合理的な手順を教師にも問うようにして下さい。

それでもダメなら、私に質問を送ってくださいね！

帝京大学以上しか受けない人等のこの問題を簡単だと思った人は、今あなたがやっているレベルをこのように解いてみてください。

きっとルールが見えてきて、今あなたがやっている問題でつまずくことが無くなるはずです。

「参考書の解法はルールがない！なんでこの問題だけ変な解き方をするの？」といった意見をよく聞きます。

決してこねくりまわすことなく、書きすぎることなく、かといって止まることもなく、「言葉からの反射」「図からの反射」で簡潔に考える修正をつけましょう。話が長くなると、自分が混乱しちゃいますよ？

【コラム】読解力と図の活用
（２）～（５）、苦手な人が多いようです。

正直なところ、これはご三家レベルの問題も混ざっていました。

逆に言えば、ここで覚えておけば、志望校を

「ご三家、国公立！」

に今から変えても大丈夫ですよ！？

さて。

いきなり(１)も、いつもの(３)レベルだったわけですが、まず、今回の(３)。これが難しいですよね？

ですが、この連載記事や門脇メソッドはそもそも、「言葉からの反射」で、難関な医学部の問題を教科書の公式だけで反射的に解くといことですので、難しい問題にこそ、真価を発揮します！

この点について、次回は深く掘り下げていきます！

【終わりに】
医学部の物理ですら、九九しかできない人が１ヶ月位で勉強を終えてしまうことが可能です。

数学すら簡単な東海大学なので、物理は本当に簡単です。今後も、効率よく勉強して、はやくお医者さんになりましょう！

「言葉からの反射」を使って、出来る限りシンプルに考える習慣を付けましょう！

勉強のやる気が無くなってしまう大きな原因に「飽きる」があります。

反射的に処理して、表にして、1分間でどんどんまとめていく習慣をつけましょう。理解速度が上がりすぎて、勉強せずにはいられなくなりますよ！！　＾O＾

より詳しい説明がほしい方は、いつでもコメント下さい！

また、解説して欲しい問題も、募集しています。