2016年7月の記事

メディカルクオークグループの代表を務める門脇先生が数学と理科の特別授業を行います。

難易度の高い問題も簡単に解りやすく解説してくれます。

授業を通じて効率の良い学習法・解法を身につけていきましょう。

第２０回．特別授業－医学部物理解法（東海大学物理2013年第３問）

【タイトル】
〜(５)になると解けなくなる？〜

「言葉からの反射」で、難関な医学部の問題を教科書の公式だけで反射的に解く

【前説】
今回は、医学部受験の入門大学として人気な東海大学。その中でも、物理を例にとって説明します。

【門脇メソッド】
「言葉からの反射」未修分野でも、閃ける

今回の(５)は難しいです。東海大学としては、難しい問題を作ったといえるでしよう。でも、見たことが無い問題、公式の繋ぎ方が未修の問題こそ実力に差がつくのが、言葉からの反射です。言葉からの反射を忠実にやりましょう。

そうすると・・・

【対象の学力層】
(上級～中級ランクまでしか受けない人は、「終わりに」の前から読んで下さい)

言葉からの反射を使って、医学部の入試問題を教科書に載っている単純な公式まで分解していきます！

今日から、医学部レベルの学力を「分単位！！」で身に着けていきましょう。

【物理の対策】
「言葉からの反射」に入る前に、今回は、物理の対策について説明しますね！ 今日は物理なので、

知識、知識の関連性	最少、多い
論理展開	中

と言えます。

こういう科目は、「言葉からの反射」が全てです。東海大学なら、平易な公式集か、そもそも教科書の裏表紙で十分でしょう。

では、解く＆覚えていきましょう。

レベル１レベル２　では非常に単純化していきましょう＋言葉からの反射表を作っていきましょう。

【問題】
空気中に置かれた図のような長さl［ｍ］の開管と閉管がある。

これらの管内の気柱を伝わる音波がつくる定常波について以下の各問に答えなさい。

答えは各問の解答群の中から最も適切なものを一つ選び、解答欄の記号にマークしなさい。

ただし、開口端と定常波の腹の位置とは一致するものとし、必要があれば温度t［℃］のときの空気中の音速v［m/s］を求める式、v=331.5＋0.6tを用いなさい。

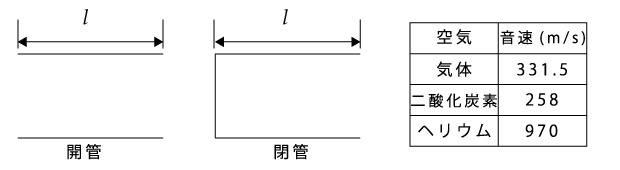
はじめに２つの管を温度0℃の空気中に置いた。

（１） 開管と閉管にできる定常波の基本振動数が△f［Hz］であった。開管および閉管の長さl［m］を求めなさい。
（２） 開管にできる定常波の2倍振動と閉管にできる3倍振動の場合の波長の差は何mか。
（３） 開管を0℃の空気中においた場合、0℃の二酸化炭素中においた場合、0℃のヘリウム中においた場合で、基本振動数の定常波ができるとき、振動数の大きさの順序はどのようになるか。ただし、0℃のときの各気体の音速は票の通りである。

次に、空気中に置かれた開管と気柱の温度をt［℃］に上昇させた。

（４） 温度がt1［℃］の場合と0℃の場合の開管にできる定常波の基本振動数の差は何Hzか。ただし、ここでは管の熱膨張は考えないものとする。
（５） 温度上昇に伴う開管の熱膨張を考慮してみよう。
温度上昇によっても定常波の基本振動数が0℃の場合と変わらないようにするには、管の線膨張率α［1/K］はどのくらいの値が必要か。最も近いものを求めなさい。

なお、今回は波動の問題です。

波動は、公式が少ない＝読解力が問われるジャンルです。

（1）
開管・閉管の長さ＝？
基本振動数の差を使う
基本振動数の差＝f1-f2
ｖ＝ｆλ
λ
：開管
1/2　λ＝ｌ
：閉管
1/4　λ＝ｌ
ｖ＝331.5
代入して計算すると、

（2）
波長の差＝？
λ
：開管の２倍振動
1/2　λ3　×2＝ｌ
：閉管の３倍振動
1/4　λ4　☓3＝ｌ
代入して計算すると、

（3）振動数の順番
ｖ＝ｆｌを使う
ｖの順番
ヘリウム＞空気＞二酸化炭素

（4）
基本振動数の差＝？
０℃の基本指導数は
331.5＝ｆ0・2l
だった
すると、
ｔ１℃の基本指導数は
331.5+0.6t＝ｆ(t)・2l
となることがわかる
代入して計算すると、

（5）
読解力が必要である。
温度上昇の前後を比較すればヨイ
α＝？
基本振動数の差を比較しろと書いてある
０℃の基本指導数は
331.5＝ｆ0・2l
ｔ１℃の基本指導数は
331.5+0.6t＝ｆ(t)・2l
だった
熱膨張を考慮するとｔ１℃の管の長さが変わるので、２ｌが変わる
αの単位が[ 1/K ]とあるので、
l1＝l0（1＋αｔ)
代入して計算すると、

答えとしては、
イウウウエ
となる。

こんなにシンプルに出来ちゃいます。

普段から解説を読んだり予備校で聞いたりしてると思います。

それは行き当たりばったりの解法であることが多いので、より合理的な手順を教師にも問うようにして下さい。それでもダメなら、私に質問を送ってくださいね！

帝京大学以上しか受けない人等のこの問題を簡単だと思った人は、今あなたがやっているレベルをこのように解いてみてください。

きっとルールが見えてきて、今あなたがやっている問題でつまずくことが無くなるはずです。

「参考書の解法はルールがない！なんでこの問題だけ変な解き方をするの？」といった意見をよく聞きます。

決してこねくりまわすことなく、書きすぎることなく、かといって止まることもなく、「言葉からの反射」「図からの反射」で簡潔に考える修正をつけましょう。話が長くなると、自分が混乱しちゃいますよ？

【終わりに】
医学部の物理ですら、九九しかできない人が１ヶ月位で勉強を終えてしまうことが可能です。数学すら簡単な東海大学なので、物理は本当に簡単です。今後も、効率よく勉強して、はやくお医者さんになりましょう！

「言葉からの反射」を使って、出来る限りシンプルに考える習慣を付けましょう！

勉強のやる気が無くなってしまう大きな原因に「飽きる」があります。反射的に処理して、表にして、1分間でどんどんまとめていく習慣をつけましょう。

理解速度が上がりすぎて、勉強せずにはいられなくなりますよ！！　＾O＾

より詳しい説明がほしい方は、いつでもコメント下さい！また、解説して欲しい問題も、募集しています。

第２１回．特別授業－医学部物理解法（東海大学物理2013年第４問）

【タイトル】
〜簡単な問題から時間を集める、元気玉の発想？〜

「言葉からの反射」で、難関な医学部の問題を教科書の公式だけで反射的に解く

【前説】
今回は、医学部受験の入門大学として人気な東海大学。その中でも、物理を例にとって説明します。

【門脇メソッド】
「言葉からの反射」未修分野でも、閃ける

今回は最高にカンタンです。こういう時には、他の問題に時間を裂けるように、スピードを上げる「元気玉の発想」で臨みましょう。なお、順番としては、他の問題を何か説いた後に着手したほうが、「調子に乗らなくて」オススメです。

そうすると・・・

【対象の学力層】
(上級～中級ランクまでしか受けない人は、「終わりに」の前から読んで下さい)

言葉からの反射を使って、医学部の入試問題を教科書に載っている単純な公式まで分解していきます！

今日から、医学部レベルの学力を「分単位！！」で身に着けていきましょう。

【物理の対策】
「言葉からの反射」に入る前に、今回は、物理の対策について説明しますね！ 今日は物理なので、

知識、知識の関連性	最少、多い
論理展開	中

と言えます。

こういう科目は、「言葉からの反射」が全てです。東海大学なら、平易な公式集か、そもそも教科書の裏表紙で十分でしょう。

では、解く＆覚えていきましょう。

レベル１レベル２　では非常に単純化していきましょう＋言葉からの反射表を作っていきましょう。

【問題】
質量500gで比熱0.40J／(g・K)の物体A、質量1000gで比熱0.50J／(g・K)の物体B、質量500gで比熱1.0J／(g・K)の物体Cがある。熱のやりとりに関する以下の各問に答えなさい。

（１） 物体Aの熱容量は何J／(g・K)か。
（２） 物体Aの温度を25℃から150℃まで上げるとき、必要な熱量は何Jか。
（３） 温度が150℃の物体Aを、温度が10℃の物体Bに接触させ、熱平衡に達したとき、物体Bの温度は何℃になるか。ただし、熱のやりとりは、物体Aと物体Bの間のみで起こるものとする。

電熱器を使用して物体Cを温めた。電熱器の電熱線には、直流の電圧100Vをかけて、0.50Aの電流を流した。

（４） この電熱器で物体Cの温度を30℃から210℃まで温めるのにかかる時間は何sか。ただし、電熱器の熱はすべて物体Cに伝わるものとし、まわりに熱は逃げないものとする。
（５） （４）において、電熱器が消費した電力量は何Kwhか。

なお、今回は熱容量の問題です。

熱容量は、単位さえわかっていれば受験物理最高にカンタンな問題ジャンルです。センター試験でもほぼ同じ問題が出題されています。

（1）
J/K＝？
[J/K]=[g・K] [g]
代入して計算すると、

（2）
J＝？
[J]= [J/K][K]
代入して計算すると、

（3）
物体Bの℃=?
熱平衡：150℃の物体A、10℃の物体B
全体の[J/k]
半分がBに使われるから、
代入して計算すると、

（4）
[s]＝？
[s]:[J]=[W][s],[W]=[V][A]
代入して計算すると、

（5）
[kWh]=?
[kWh]=10^3・3600[J]
代入して計算すると、

答えとしては、
2.0×10^2
2.5×10^4
50
1.8×10^3
2.5×10^-2
となる。

こんなにシンプルに出来ちゃいます。

普段から解説を読んだり予備校で聞いたりしてると思います。

それは行き当たりばったりの解法であることが多いので、より合理的な手順を教師にも問うようにして下さい。

それでもダメなら、私に質問を送ってくださいね！

帝京大学以上しか受けない人等のこの問題を簡単だと思った人は、今あなたがやっているレベルをこのように解いてみてください。

きっとルールが見えてきて、今あなたがやっている問題でつまずくことが無くなるはずです。

「参考書の解法はルールがない！なんでこの問題だけ変な解き方をするの？」といった意見をよく聞きます。

決してこねくりまわすことなく、書きすぎることなく、かといって止まることもなく、「言葉からの反射」「図からの反射」で簡潔に考える修正をつけましょう。話が長くなると、自分が混乱しちゃいますよ？

【終わりに】
医学部の物理ですら、九九しかできない人が１ヶ月位で勉強を終えてしまうことが可能です。

数学すら簡単な東海大学なので、物理は本当に簡単です。今後も、効率よく勉強して、はやくお医者さんになりましょう！

「言葉からの反射」を使って、出来る限りシンプルに考える習慣を付けましょう！

勉強のやる気が無くなってしまう大きな原因に「飽きる」があります。反射的に処理して、表にして、1分間でどんどんまとめていく習慣をつけましょう。

理解速度が上がりすぎて、勉強せずにはいられなくなりますよ！！　＾O＾

より詳しい説明がほしい方は、いつでもコメント下さい！また、解説して欲しい問題も、募集しています。

第２２回．特別授業－医学部物理解法（東海大学物理2012年第1問）

【タイトル】
〜簡単な問題から時間を集める、元気玉の発想？〜

「言葉からの反射」で、難関な医学部の問題を教科書の公式だけで反射的に解く

【前説】
今回は、医学部受験の入門大学として人気な東海大学。その中でも、物理を例にとって説明します。

【門脇メソッド】
「言葉からの反射」未修分野でも、閃ける

今回は最高にカンタンです。こういう時には、他の問題に時間を裂けるように、スピードを上げる「元気玉の発想」で臨みましょう。

なお、順番としては、他の問題を何か説いた後に着手したほうが、「調子に乗らなくて」オススメです。

そうすると・・・

【対象の学力層】
(上級～中級ランクまでしか受けない人は、「終わりに」の前から読んで下さい)

言葉からの反射を使って、医学部の入試問題を教科書に載っている単純な公式まで分解していきます！

今日から、医学部レベルの学力を「分単位！！」で身に着けていきましょう。

【物理の対策】
「言葉からの反射」に入る前に、今回は、物理の対策について説明しますね！ 今日は物理なので、

知識、知識の関連性	最少、多い
論理展開	中

と言えます。

こういう科目は、「言葉からの反射」が全てです。東海大学なら、平易な公式集か、そもそも教科書の裏表紙で十分でしょう。

では、解く＆覚えていきましょう。

レベル１レベル２　では非常に単純化していきましょう＋言葉からの反射表を作っていきましょう。

【問題】
図１、図２のようなxy平面上で、質量mの小球Aを、x軸上に置いた質量M（M＞m）の小球Bにさまざまな条件で衝突させた。

以下の問いに答えなさい。
ただし、衝突時における小球の変形や摩擦は無視する。

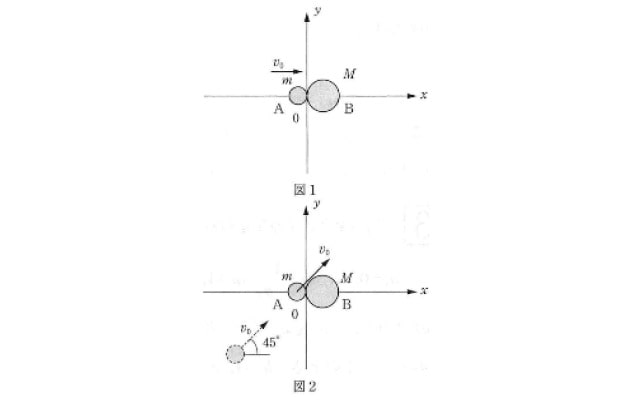
図１のように小球Aを、x軸上の正の向きに速さv₀で、自由に動ける状態で静止している小球Bと衝突させた。衝突は弾性衝突であった。

（１） 小球Aの衝突後の速さを求めなさい。

（２） 小球Bの衝突後の速さを求めなさい。

次に、図２のように小球Bをx軸上に固定した状態で、小球Aを速さv₀で速度の向きがx軸の正の向きと45℃の角をなすよう小球Bに向かって運動させた。小球Aと小球Bはx軸上で弾性衝突した。

（３） 小球Aの衝突後の速度のx成分とy成分を求めなさい。

さらに、小球Aと小球Bの材料を変え、質量はそれぞれm、M（M＞m）とし、図２において小球Bを自由に動けるような状態で静止させた。再び小球Aをx軸とのなす角が45℃となるよう速さv₀で小球Bに衝突させた。このときのはねかえり係数をe（＜1）とする。

（４） 小球Aの衝突後の速度のx成分とy成分を求めなさい。

（５） 小球Bの衝突後の速度のx成分とy成分を求めなさい。

なお、今回は運動量の問題です。保存則と弾性衝突の法則を、「運動量セット」にして使いましょう。

熱容量は、単位さえわかっていれば受験物理最高にカンタンな問題ジャンルです。センター試験でもほぼ同じ問題が出題されています。

（1）
衝突後の速さ＝？
速さ：速度の絶対値
衝突後の速さ：運動量セット
代入して計算すると、
その絶対値は、

（2）
（１）と同じ
（１）に代入して計算すると、

（3）
速度のｘ成分、ｙ成分：運動量セットを、ｘ成分、ｙ成分
eが使えるのはｘ成分だけ
ｘ成分だけやってみる
代入して計算すると、
偶然終わる

（4）
速度のｘ成分、ｙ成分：運動量セットを、ｘ成分、ｙ成分
代入して計算すると、

（5）
（４）と同じ
（４）に代入して計算すると、

答えとしては、
（M-m　/　m+M）v0
（2m　/　m+M）v0
-v0/√2、v0/√2
（m-eM　/　√2(m+M)）v0、v0/√2
（M-m　/　m+M）v0、０
となる。

こんなにシンプルに出来ちゃいます。

普段から解説を読んだり予備校で聞いたりしてると思います。

それは行き当たりばったりの解法であることが多いので、より合理的な手順を教師にも問うようにして下さい。それでもダメなら、私に質問を送ってくださいね！

帝京大学以上しか受けない人等のこの問題を簡単だと思った人は、今あなたがやっているレベルをこのように解いてみてください。

きっとルールが見えてきて、今あなたがやっている問題でつまずくことが無くなるはずです。

「参考書の解法はルールがない！なんでこの問題だけ変な解き方をするの？」といった意見をよく聞きます。

決してこねくりまわすことなく、書きすぎることなく、かといって止まることもなく、「言葉からの反射」「図からの反射」で簡潔に考える修正をつけましょう。話が長くなると、自分が混乱しちゃいますよ？

【終わりに】
医学部の物理ですら、九九しかできない人が１ヶ月位で勉強を終えてしまうことが可能です。

数学すら簡単な東海大学なので、物理は本当に簡単です。

今後も、効率よく勉強して、はやくお医者さんになりましょう！

「言葉からの反射」を使って、出来る限りシンプルに考える習慣を付けましょう！

勉強のやる気が無くなってしまう大きな原因に「飽きる」があります。

反射的に処理して、表にして、1分間でどんどんまとめていく習慣をつけましょう。理解速度が上がりすぎて、勉強せずにはいられなくなりますよ！！　＾O＾

より詳しい説明がほしい方は、いつでもコメント下さい！また、解説して欲しい問題も、募集しています。

第２３回．特別授業－医学部物理解法（東海大学物理2012年第2問）

【タイトル】
〜公式一発で解けないなら、義務教育の数学。〜

「言葉からの反射」で、難関な医学部の問題を教科書の公式だけで反射的に解く

【前説】
今回は、医学部受験の入門大学として人気な東海大学。その中でも、物理を例にとって説明します。

難関医学部受ける人も、今日の東海大学の問題は価値ありますよ！

【門脇メソッド】
「言葉からの反射」未修分野でも、閃ける

今回は難しいです。問題自体は簡単なんですが、「言葉からの反射」が公式一発でしか使えないあなた、ちょっと難しいです。必ず読んで下さい。

こういう時には、公式の範囲を義務教育レベルの数学まで広げてみましょう。

そうすると・・・

【対象の学力層】
今日は、読んだほうがヨイでしょう。(上級～中級ランクまでしか受けない人は、「終わりに」の前から読んで下さい)

言葉からの反射を使って、医学部の入試問題を教科書に載っている単純な公式まで分解していきます！

今日から、医学部レベルの学力を「分単位！！」で身に着けていきましょう。

【物理の対策】
「言葉からの反射」に入る前に、今回は、物理の対策について説明しますね！ 今日は物理なので、

知識、知識の関連性	最少、多い
論理展開	中

と言えます。

こういう科目は、「言葉からの反射」が全てです。東海大学なら、平易な公式集か、そもそも教科書の裏表紙で十分でしょう。

では、解く＆覚えていきましょう。

レベル１レベル２　では非常に単純化していきましょう＋言葉からの反射表を作っていきましょう。

【問題】
電子が電場及び磁場によりどの様に曲げられるかを観測するために２つの実験装置を準備した。

図１は電場を、図２は磁場を用いた装置を示している。

両図において左側から電子を一定の速さvで原点Oからz方向に入射した。図１では長さlの2枚の電極版がz軸に平行に置かれている。

電極版には電池がつながれており極板間の電場の大きさはEである。

図2では長さlの灰色の領域に磁束密度Bの磁場が紙面の裏から表に向かって紙面に垂直にかけられている。

ただし、電場及び磁場は一様であり、端の部分の歪みはないものとする。電子の電気量の大きさをe、質量をmとする。

電子が電場及び磁場から受ける力に比べて重力は小さく無視できるものとして、次の各問いに答えなさい。

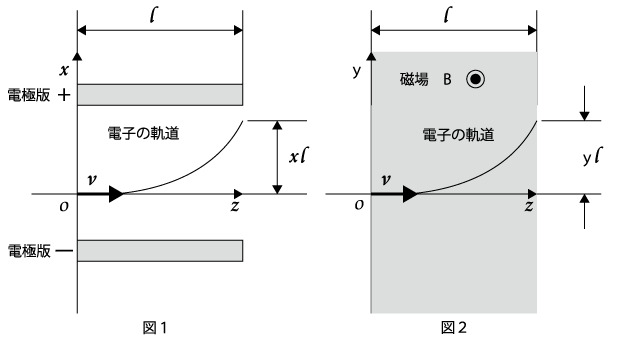
図１において電子はx方向に変位する。

（１） 電子の受けるx方向の力の大きさを求めなさい。

（２） ｚ＝ｌの位置で電子のx座標xlを求めなさい。

図2において電子は等速円運動をし、y方向を変位する。

（３） 電子の円運動の半径を求めなさい。

（４） ｚ＝ｌの位置で電子の通過するy座標ylを求めなさい。

（５） （２）と（４）で求めたxlとylに現れるvを消去すると、電子の比電荷（e/m）を求めることができる。e/mをxlとylを用いて表しなさい。

ただし、電子の回転半径に比べて磁場のかけられている範囲の長さlは小さいと考え、aが１に比べて十分に小さい時に成り立つ近似式、√１－ａ≒１－ａ/２を利用しなさい。

なお、今回は運動量の問題です。保存則と弾性衝突の法則を、「運動量セット」にして使いましょう。

（1）
電子の受ける力の大きさ＝？
F=qE　か　F＝qvB
前者を選択(∵もちろん、簡単だから)
代入して計算すると、

（2）
電子の座標＝？
公式、無い
座標：運動３式　a,v,x,tが有ることを確認
ｔだけ無い：ｔを他のもので表す
代入して計算すると、

（3）
電子の円運動の半径：電子の円運動の半径の公式
代入して計算すると、

（4）
コラム参照

（5）
計算するだけ。(計算の工夫として、置換するとヨイ)
代入して計算すると、

答えとしては、
eE
eEl^2 / 2mv^2
mv / eB
mv / eB – √(m^2v^2 / e^2B^2 – l^2)
2E / b^2l^2 ・ yl^2 / xl

となる。

こんなにシンプルに出来ちゃいます。

普段から解説を読んだり予備校で聞いたりしてると思います。

それは行き当たりばったりの解法であることが多いので、より合理的な手順を教師にも問うようにして下さい。

それでもダメなら、私に質問を送ってくださいね！

帝京大学以上しか受けない人等のこの問題を簡単だと思った人は、今あなたがやっているレベルをこのように解いてみてください。

きっとルールが見えてきて、今あなたがやっている問題でつまずくことが無くなるはずです。

「参考書の解法はルールがない！なんでこの問題だけ変な解き方をするの？」といった意見をよく聞きます。

決してこねくりまわすことなく、書きすぎることなく、かといって止まることもなく、「言葉からの反射」「図からの反射」で簡潔に考える修正をつけましょう。話が長くなると、自分が混乱しちゃいますよ？

【コラム】公式一発で解けないなら、義務教育の数学。
（４）ですが、

（２）共々、いつもの東海大学のLevelからすると難しいですね。
まず、論理展開ですが、

（２）と同じ方法で解きたい
円運動だからダメ
図で解く(中学レベルの数学で考える)
代入して計算すると、

という流れになります。

全体として、当然、「言葉からの反射」で処理するのが基本

ただ、公式一発で解けることがほとんどの、問題自体は簡単な私大医学部(慶應はもちろん除く)。

上位国立や慶應の医学部になると早慶以上の難易度が出題されますが、そこまででもない私大医学部。

その私大医学部に出題された「公式一発を繋ぐだけで解ける問題」ではない問題を解くときは、同じ「言葉からの反射」でも、公式を言葉に合わせて充てがうだけでは解けません。

では、どうするか。

そういう時は、簡単な数学を使いましょう。小学校、中学校の知識を使いましょう。

上位国立や慶應を相手にするときは、微積以上の数学を除く高校数学が必要な問題も有りますが、私大医学部にはそこまでは必要ありません。

義務教育か一流高校受験レベルの数学でほぼ十分です。

【終わりに】
医学部の物理ですら、九九しかできない人が１ヶ月位で勉強を終えてしまうことが可能です。数学すら簡単な東海大学なので、物理は本当に簡単です。今後も、効率よく勉強して、はやくお医者さんになりましょう！

「言葉からの反射」を使って、出来る限りシンプルに考える習慣を付けましょう！

勉強のやる気が無くなってしまう大きな原因に「飽きる」があります。反射的に処理して、表にして、1分間でどんどんまとめていく習慣をつけましょう。理解速度が上がりすぎて、勉強せずにはいられなくなりますよ！！　＾O＾

より詳しい説明がほしい方は、いつでもコメント下さい！また、解説して欲しい問題も、募集しています。