2016年5月の記事

メディカルクオークグループの代表を務める門脇先生が数学と理科の特別授業を行います。

難易度の高い問題も簡単に解りやすく解説してくれます。

授業を通じて効率の良い学習法・解法を身につけていきましょう。

第１３回．特別授業－医学部数学解法（東海大学数学2012年第2問）

【タイトル】
〜先入観と戦え！！〜

「言葉からの反射」で、難関な医学部の問題を教科書の公式だけで反射的に解く

【前説】
今回は、医学部受験の入門大学として人気な東海大学。その中でも最もメジャーな加もすべき科目、数学を例にとって説明します。

【門脇メソッド】
「質問されているから値を出さなくてはいけないという先入観」ではなく、「あくまでも与えられているものは全部課程だから使える」

難しく見える題材も、問題文が簡単なら大丈夫。「言葉からの反射」を使って、反射的に処理できますよ。

【対象の学力層】
(上級～中級ランクまでしか受けない人は、「終わりに」の前から読んで下さい)

言葉からの反射を使って、医学部の入試問題を教科書に載っている単純な公式まで分解していきます！

今日から、医学部レベルの学力を「分単位！！」で身に着けていきましょう。

【数学の対策】
「言葉からの反射」に入る前に、今回は、数学の対策について説明しますね！

数学は、

知識、知識の関連性	少ない、多い
論理展開	大

と言えます。

こういう科目は、「言葉からの反射」と多岐に渡る可能性の比較が重要です。ただ、東海大学なら、センター試験程度で十分でしょう。

では、解く＆覚えていきましょう。

レベル１レベル２　では非常に単純化していきましょう＋言葉からの反射表を作っていきましょう。

は、紙面の関係で割愛した。

ところで今回の問題は、区分求積法という、数学が苦手な生徒が恐れる分野ワースト３級の範囲です。しかし、難しい分野の方が、問題自体は簡単なものです。 それでは、始めましょう。

【問題】

(2) AB=BC=1、∠B=π2である直角二等辺三角形ABCがある。nを2以上の整数とする。辺BC上にn個の点P1, P2, ⋯, Pnがあり、

となっている。ｎ、ｋで表すとAPｋ=イ、BPｋ=ウである。区分求積法により

である。積分の値を求めれば、

である。また

である。

(1)
「log の分数の微分」という風に言葉にしてしまうと、簡単に着手できる。

logの微分、これは「y’/y」である

「y’」は分数の微分になるので、「分数の微分の公式」を使う。

「計算テクニック」として 「値は最後まで代入しない」が基本なので、「分数の微分の公式」の「ｆ」,[g]をそのまま残すことをオススメする。答えは最後に示した。

(2)
この問題を見た瞬間に、「難しい」と考えて捨ててしまった人が多いと思われる。

しかしながら、こういうふうに一見難しく見える問題でも、いつもどおりの手順で処理することが可能だ。

APｋ BPｋ を問われているので図を書いてみる。図を書いてみるとそれぞれを三角比で表せることが分かるので、それをそのまま利用すれば良い。

ここでポイントなのは、「質問されているから値を出さなくてはいけないという先入観」ではなく、「あくまでも与えられているものは全部課程だから使える」という考え方をすることだ。

つい気になってしまうが、こういう心理的な罠に引っかからないようにしたい。

エ
区分求積法と書いてあるので区分求積法を書いてみる。

ここでポイントなのは、区分求積法であるということ 。

「区分求積法」という言葉を見た瞬間に、ビビって「難しい」と考えて捨ててしまった人はかなり多いであろう。

こういう心理的なテクニックに騙されないようにしたい。

「難しい題材の問題は簡単」

公式を書いてみれば分かるように 、既に「k/n」の部分が与えられている。(公式：lim(n→∞) 1/n Σ(n,k=1) f (k/n) = ∫(1,0)f(x)dx)

ここを、「目で見たまま比べる」を使えば十分である。

「k/n」の部分を「ｘ」に変えればいいので、この形となる。

オ
tanの積分は「-cos」であるが、このままでは計算出来ない。
そこで、tanの中身を置換する。

カ
同様に式を立ててみると、この形となる。

（∫(1,0) dx/(cos π/4 x)

この「π/4」の部分は置換できることがわかっているので、一旦置換してみる。すると・・・！

なんと、（１）と同じである。

よって、ココで初めて（１）の利用ができる。

ということになって、積分して進めていく。

最終的な答えは、こうなる。
（1）

cos x

（２）
1/(cos kπ/4n)
tan kπ/4n
tan π/4 x
2log 2/π
4/π log(1+ﾙｰﾄ2)

まとめ
今回の問題でもあったように、

① まずは言葉からの反射。そこに公式があって、

② 手詰まりになったら他の公式を使う
a計算が困っている場合は置換するなどの計算の公式を使えば良いし、
bそうでない場合は、ほかの課程などから持ってきて公式を追加すればいい。

また、
「（１）は利用する」
「質問されているから値を出さなくてはいけないという先入観」ではなく、「あくまでも与えられているものは全部課程だから使える」
などを学んだ。

さて、今回は、先入観と戦う問題でした。

「言葉からの反射」、「図からの反射」ももちろん使います。そうやっていつもどおり反射的に解きながら、「先入観と戦え！！」です。焦らず、話の流れ通りに、言葉通りに図・式を書きましょう。

帝京大学以上しか受けない人等のこの問題を簡単だと思った人は、今あなたがやっているレベルをこのように解いてみてください。きっとルールが見えてきて、今あなたがやっている問題でつまずくことが無くなるはずです。

「参考書の解法はルールがない！なんでこの問題だけ変な解き方をするの？」といった意見をよく聞きます。決してこねくりまわすことなく、書きすぎることなく、かといって止まることもなく、「言葉からの反射」「図からの反射」で簡潔に考える修正をつけましょう。話が長くなると、自分が混乱しちゃいますよ？

【終わりに】
医学部の数学ですら、九九しかできない人が１ヶ月位で勉強を終えてしまうことが可能です。特に数学と言えども、東海大学は本当に簡単です。今後も、効率よく勉強して、はやくお医者さんになりましょう！

数学が得意でも、図形が苦手な人は多いです。でも、図を描いてみると、反射的に公式が浮かぶものが多いのです。

勉強のやる気が無くなってしまう大きな原因に「飽きる」があります。反射的に処理して、表にして、1分間でどんどんまとめていく習慣をつけましょう。理解速度が上がりすぎて、勉強せずにはいられなくなりますよ！！　＾O＾

より詳しい説明がほしい方は、いつでもコメント下さい！また、解説して欲しい問題も、募集しています。

第１４回．特別授業－医学部数学解法（東海大学数学2013年第2問）

【タイトル】
〜時間との勝負は「元気玉」の発想〜

「言葉からの反射」で、難関な医学部の問題を教科書の公式だけで反射的に解く

【前説】
今回は、医学部受験の入門大学として人気な東海大学。その中でも最もメジャーな加もすべき科目、数学を例にとって説明します。

【門脇メソッド】
「一旦後回しにして他の問題から少しずつ時間を集める」という、「元気玉」の発想

受験は、人生の縮図。何より時間が大切です。「言葉からの反射」を使って反射的に処理して、時間を生み出しましょう。また、普段から自分の速度を把握しておきましょう。

【対象の学力層】
(上級～中級ランクまでしか受けない人は、「終わりに」の前から読んで下さい)

言葉からの反射を使って、医学部の入試問題を教科書に載っている単純な公式まで分解していきます！

今日から、医学部レベルの学力を「分単位！！」で身に着けていきましょう。

【数学の対策】
「言葉からの反射」に入る前に、今回は、数学の対策について説明しますね！

数学は、

知識、知識の関連性	少ない、多い
論理展開	大

と言えます。

こういう科目は、「言葉からの反射」と多岐に渡る可能性の比較が重要です。ただ、東海大学なら、センター試験程度で十分でしょう。

では、解く＆覚えていきましょう。

レベル１レベル２　では非常に単純化していきましょう＋言葉からの反射表を作っていきましょう。

は、紙面の関係で割愛した。

ところで今回の問題は、（３）の計算量が多いです。計算は一見疎かにしがちですが、物理的に限界が発生する部分でもあるので、「一旦後回しにして他の問題から少しずつ時間を集める」という、「元気玉」の発想で対処しましょう。それでは、始めましょう。

【問題】

(1)
ア　
微分公式

イ　
接線の公式

ウ　
lim(ｘ→∞) x/ e^x
こういう形が出てくるがこれは分母の方が発散速度が早いので0

(2)
エ
イコールで結ぶと x が消せる
（x の値の1つが0であることは家庭として書かれているので問題ない）

↓

指数に x が含まれている

↓

対数関数にして計算する

オ
積分公式
ｆ(x)の積分の方は難しいので、部分積分の公式

(3)
言われたとおり図を描く ※コラム参照

↓

質問されているもの の式が出る
V=∫(1/e,0)πx^2dy

↓

置換積分の公式
このままでは計算できないので。
また、この段階で　カ　と　キ　が登場する

↓

カ　部分積分の公式
途中(2)の途中式を利用する形が出てくる

↓

キ　部分積分の公式
途中　カ　の 途中式を利用する形が出てくる

↓

カ　キ　を代入して v を出す

コラム

(2)と(3)は、共に積分の問題である。

積分の問題ということは、図を書くor書かないの判断に迫られる。
(3)は図が必要と考えられる

仮定に3個の式があるが、最初の式は概形を知らない前提だ。
こういう場合、残り2つを図にしてみて、そこからもう一つが偶然見つかるという流れになる

こういう論理展開(予想)をして 勇気をもって進んでほしい。

最終的な答えは、こうなる。

(1)
ア　–(x-1)e^-x

イ　X

ウ　0

(2)
エ　2

オ　1-5/e^2

(3)
カ　2-5/e

キ　6-16/e

ク　π(11/e-4)

まとめ

さて、今回は、計算量と戦う問題でした。

「言葉からの反射」、「図からの反射」ももちろん使います。そうやっていつもどおり反射的に解きながら、「計算量と戦う」です。

「一旦後回しにして他の問題から少しずつ時間を集める」という、「元気玉」の発想で臨みましょう。

帝京大学以上しか受けない人等のこの問題を簡単だと思った人は、今あなたがやっているレベルをこのように解いてみてください。

きっとルールが見えてきて、今あなたがやっている問題でつまずくことが無くなるはずです。

「参考書の解法はルールがない！なんでこの問題だけ変な解き方をするの？」といった意見をよく聞きます。

決してこねくりまわすことなく、書きすぎることなく、かといって止まることもなく、「言葉からの反射」「図からの反射」で簡潔に考える修正をつけましょう。話が長くなると、自分が混乱しちゃいますよ？

【終わりに】
医学部の数学ですら、九九しかできない人が１ヶ月位で勉強を終えてしまうことが可能です。特に数学と言えども、東海大学は本当に簡単です。今後も、効率よく勉強して、はやくお医者さんになりましょう！

数学が得意でも、図形が苦手な人は多いです。でも、図を描いてみると、反射的に公式が浮かぶものが多いのです。

勉強のやる気が無くなってしまう大きな原因に「飽きる」があります。反射的に処理して、表にして、1分間でどんどんまとめていく習慣をつけましょう。理解速度が上がりすぎて、勉強せずにはいられなくなりますよ！！　＾O＾

より詳しい説明がほしい方は、いつでもコメント下さい！また、解説して欲しい問題も、募集しています。

第１５回．特別授業－医学部数学解法（東海大学数学2013年第2問【2】前半）

【タイトル】
〜数列、その合理的な解き方〜

「言葉からの反射」で、難関な医学部の問題を教科書の公式だけで反射的に解く

【前説】
今回は、医学部受験の入門大学として人気な東海大学。その中でも最もメジャーな加もすべき科目、数学を例にとって説明します。

【門脇メソッド】
「手が止まったら後回し」
受験は、人生の縮図。何より時間が大切です。「言葉からの反射」を使って反射的に処理して、時間を生み出す必要があるのに手が止まった。そういう時は、後回しにしましょう。そして、最後に考えましょう。そうすると・・・

【対象の学力層】
(上級～中級ランクまでしか受けない人は、「終わりに」の前から読んで下さい)

言葉からの反射を使って、医学部の入試問題を教科書に載っている単純な公式まで分解していきます！

今日から、医学部レベルの学力を「分単位！！」で身に着けていきましょう。

【数学の対策】
「言葉からの反射」に入る前に、今回は、数学の対策について説明しますね！

数学は、

知識、知識の関連性	少ない、多い
論理展開	大

と言えます。

こういう科目は、「言葉からの反射」と多岐に渡る可能性の比較が重要です。ただ、東海大学なら、センター試験程度で十分でしょう。

※【数列の対策】

レベル１レベル２　では非常に単純化していきましょう＋言葉からの反射表を作っていきましょう。

あまり科目や分野を特別視したくは有りませんが、今回は泣く泣く。今回は、数列の問題です。

門脇メソッドのカリキュラムとしても、
「言葉からの反射」「規則性を見つけたら表にする」（「薄い知識をミルフィーユ」も少々）

などを学ぶためにまずは関数・図形分野に着手しますが、数列は色々なコツがあるので、別にしてまとめて取り扱っています。

なお、

「レベル１レベル２　では非常に単純化していきましょう＋言葉からの反射表を作っていきましょう。」

は、紙面の関係で割愛しました。

では、解く＆覚えていきましょう。

【問題】

(1)
「聞かれてること＝」で考えると b（n +1）を考えたい。
直接表すことができないので、他の手段を考えたい。
b(n)は表せることが分かっているので、これを使って b（n +1）を考えたい

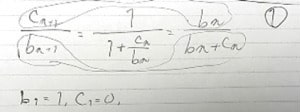
この式から、分母同士分子同士で比べることができる

(2)
イ
n が3以上のときは既に考えているので、これが n ＝1、2のときも成り立つかを考えると

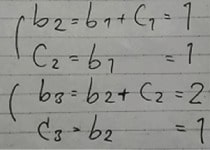
よって、すべての自然数について成り立つといえる。

ウ
【解法１】 
オススメ

この問題は、漸化式が非常にカンタンにかけるので、表にしてみる。

「聞かれていること」は　ｎ≧２　の部分だけなので表を使うとこうなる。

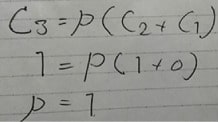
【解法２】
一般的には、こう解く人が多いと思う。
与式にbを代入。

b(n)とc(n)は互いにどちらか１つで表せることが分かっているので、どちらか１つにしたい。

c(n +1)が表されているので、c(n)、c(n-1)も表すことができる。それをするとこうなる。

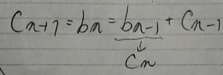
これを 与えられている 式と比べると、こうなる

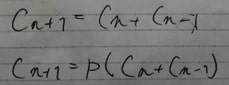
よって p ＝1

【コラム】

（２）は、驚きの解法が有った。

「言葉からの反射」を使い、手が止まることは最小限に抑えたい。これは、いつも通り。

また、いつも手が止まらずに解けるのに本番では解けない。こんなことが起きた場合、着眼点を変えてみよう。むやみに変えるのではない。

今回は、

「カンタンだから、表まで作っちゃう」

という自然な心理に従った。

最終的な答えは、こうなる。

（1）

b(n)＋c(n)

(2)

イ

b(n)

ウ

1

では、解く＆覚えていきましょう。

さて、今回は、別解がある問題でした。

解説の論理添加を覚えるのが基本ですが、「言葉からの反射」や、「手が止まったら後回し」を使い、より合理的な手順を教師にも問うようにして下さい。

それでもダメなら、私に質問を送ってくださいね！

帝京大学以上しか受けない人等のこの問題を簡単だと思った人は、今あなたがやっているレベルをこのように解いてみてください。

きっとルールが見えてきて、今あなたがやっている問題でつまずくことが無くなるはずです。

「参考書の解法はルールがない！なんでこの問題だけ変な解き方をするの？」といった意見をよく聞きます。

決してこねくりまわすことなく、書きすぎることなく、かといって止まることもなく、「言葉からの反射」「図からの反射」で簡潔に考える修正をつけましょう。話が長くなると、自分が混乱しちゃいますよ？

【終わりに】
医学部の数学ですら、九九しかできない人が１ヶ月位で勉強を終えてしまうことが可能です。特に数学と言えども、東海大学は本当に簡単です。今後も、効率よく勉強して、はやくお医者さんになりましょう！

数学が得意でも、図形が苦手な人は多いです。

でも、図を描いてみると、反射的に公式が浮かぶものが多いのです。

勉強のやる気が無くなってしまう大きな原因に「飽きる」があります。

反射的に処理して、表にして、1分間でどんどんまとめていく習慣をつけましょう。理解速度が上がりすぎて、勉強せずにはいられなくなりますよ！！　＾O＾

より詳しい説明がほしい方は、いつでもコメント下さい！また、解説して欲しい問題も、募集しています。