2016年4月の記事

メディカルクオークグループの代表を務める門脇先生が数学と理科の特別授業を行います。

難易度の高い問題も簡単に解りやすく解説してくれます。

授業を通じて効率の良い学習法・解法を身につけていきましょう。

第９回．特別授業－医学部物理解法（公式選び＋帝京大学2012物理大問1）

【タイトル】
〜 どの公式を使うかすぐに分かります？〜

「言葉からの反射」で、難関な医学部の問題を教科書の公式だけで反射的に解く

【前説】
今回は、制限時間に悩む生徒などを対象に、正しい公式を選ぶ方法を、帝京大学医学部の物理を例にとって説明します。

【門脇メソッド】
一見簡単な題材でも、公式を選び間違えると大幅ロス。「言葉からの反射」を使って出てきた選択肢のうち、どれが正しい公式か選ぶ方法を学びましょう。

【対象の学力層】
言葉からの反射を使って、医学部の入試問題を教科書に載っている単純な公式まで分解していきます！

今日から、医学部レベルの学力を「分単位！！」で身に着けていきましょう。

【物理の対策】
「正しい公式の選び方」に入る前に、まず公式の選び方を考えてみましょう。

ベストは何でしょう？

それは、「聞かれている言葉以外が、全部与えられている言葉で構成されている公式」を持ってくることなんです！

・グルコース、と聞いてどの公式(情報？予備校のテキスト？)を思い出しますか？
・面積、と聞いてどの公式を思い出しますか？
・have、と聞いた場合は？

そう、たくさんありますよね。

みんな忘れがちですが、中学校で習ったはずなんです。そして、高校で身にしみたはずなんです。未知数の個数で決めればいいと。

ただ、応用が出来ない。化学にしろ、英語にしろ、社会にしろ、正しい公式は決まっています。

では、解く＆覚えていきましょう。

ところで今回の問題は、図が有りません。簡単な問題かも？と、問題選択の時に考えてみても良いかもしれません。

しかし、簡単な問題こそ、最速の手順にこだわりましょう！

それでは、始めましょう。

【問題】

質量mmの小球を初速v0v0で鉛直上方に投げ上げた。重力加速度の大きさをggとし、以下の設問に答えよ。

空気抵抗を無視した場合、

(1) 小球が到達する最高点の高さは投げ上げた位置から測っていくらか。

(2) 最高点に到達するまでの時間はいくらか。

(3) 小球が投げ上げた位置に戻ってくるまでの時間はいくらか。

(後半省略)

では、物理、化学、数学の時と同じように、門脇メソッド「言葉からの反射」を使ってみましょう！そろそろ自身を持って使いこなせますか？前回に続いての今回は、使いこなして、選択肢が多く出てきた時の対策ですね！

問題文に書かれている言葉から、反射的に考えるのが、「言葉からの反射」でしたね。これを、全問題を通して整理すると以下のようになります。

（以前、表が画像だったので見辛い、というお問い合わせを頂いたので、表示方法を変えました！）

このようにして、正しい公式を選ぶことにこだわりましょう！

【終わりに】
医学部の物理ですら、九九しかできない人が一ヶ月位で勉強を終えてしまうことが可能です。

簡単な問題こそ、計算速度が大事になってきます。計算速度に含まれるかもしれませんが、大事なのは「正しい公式の選び方」です。

こういう時こそ、落ち着いて、「書き始める前に選択肢をさらっと２０秒で思い浮かべる」習慣を付けましょう。

「あれ？簡単に見えるってことは、落ち着いてベストを探そう」
そう思えるようなら、大丈夫。簡単に見える問題は簡単です。(※広く捉えられる言葉や複雑な言葉で構成されている問題は、簡単に見えているだけなので注意。)

勉強のやる気が無くなってしまう大きな原因に「飽きる」があります。反射的に処理して、表にして、1分間でどんどんまとめていく習慣をつけましょう。

理解速度が上がりすぎて、勉強せずにはいられなくなりますよ！！　＾O＾

より詳しい説明がほしい方は、いつでもコメント下さい！また、解説して欲しい問題も、募集しています。

第１０回．特別授業－医学部物理解法（帝京大学2013物理大問3）

【タイトル】
〜理科の計算で手こずってませんか？？〜

「言葉からの反射」で、難関な医学部の問題を教科書の公式だけで反射的に解く

【前説】
今回は、特殊な計算があったらパスしてしまう生徒などを対象に、特殊な計算が関わる理科の苦手克服を、帝京大学医学部の物理を例にとって説明します。

【門脇メソッド】
一見特殊な計算でも、いつも通りで大丈夫。「言葉からの反射」を使って特殊な計算が関わる理科の苦手克服を学びましょう。

【対象の学力層】
言葉からの反射を使って、医学部の入試問題を教科書に載っている単純な公式まで分解していきます！

今日から、医学部レベルの学力を「分単位！！」で身に着けていきましょう。

【物理の対策】
「特殊な計算が関わる理科の苦手克服」に入る前に、まず特殊計算について考えてみましょう。

ベストは何でしょう？

それは、「導入に従って反射的に解く」ことなんです！

化学にしろ、物理にしろ、生物にしろ、正しい公式は決まっています。

ところで今回の問題は、３問しか有りません。簡単な問題かも？と、問題選択の時に考えてみても良いかも知れません。

特殊な計算が関わるからパス！なんてことにならないようにしましょう！

それでは、始めましょう。

【問題】
図は可変抵抗と抵抗値rの抵抗および起電力Vの直流電源からなる回路を示している。以下の設問に答えよ。

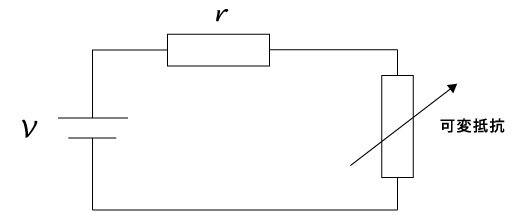
可変抵抗の抵抗値をRとすると、

(1) 回路に流れる電流の大きさはいくらか。

(2) それぞれの抵抗で消費される電力はいくらか。

(3) 可変抵抗で消費される電力Pを最大とするには、抵抗値をいくらに設定すればよいか。また、そのときの消費電力Pはいくらか。必要ならば、関係式

(x+y)2=(x−y)2+4xy≧4xy(x+y)2=(x−y)2+4xy≧4xy

を用いよ。

では、物理、化学、数学の時と同じように、門脇メソッド「言葉からの反射」を使ってみましょう！そろそろ自身を持って使いこなせますか？前回に続いての今回は、使いこなして、選択肢が多く出てきた時の対策ですね！

問題文に書かれている言葉から、反射的に考えるのが、「言葉からの反射」でしたね。これを、全問題を通して整理すると以下のようになります。

１番 V=電流×抵抗 ：抵抗・・・r＋R だから、電流＝V/(r＋R）

２番 消費電力＝（電流（２乗））×抵抗 電力（可変抵抗）：I（２乗）R＝V（２乗）R/（r＋R）（２乗） 電力（抵抗）：I（２乗）r＝V（２乗）r/（r＋R）（２乗）

３番 Pを最大とする・・・Pの式は分数・・・分母最小・・・（r＋R） （２乗）の最小・・・ヒントにある (x+y)（２乗）≧4xy (r+R）（２乗）＝４rR （計算） r（２乗）＋２rR＋R（２乗）ー４rR＝０ r（２乗）ー２rR＋R（２乗）＝０ (r-R）（２乗）＝０ r＝R P＝V（２乗）R/４r

特殊な計算が関わる理科の苦手克服

では、本題に入りましょう。

３番ですね。１番と２番は、ノンストップで合計２分で解けたと思います。

３番は、途中まで予想通り行きますが、数学が苦手な生徒は計算に手こずったようでした。

確かに、「最大」を求める方法は沢山あります。

微分？相加相乗？
分数のときは、分母＝０が簡単です。

慶應医学部でも受験しない限り、理科の計算が難しいことはありません。何パターンか計算方法が考えられる場合は、一問一答で判断できるようにまとめておきましょう。

もしくは、私に直接質問してください。

【終わりに】

医学部の物理ですら、九九しかできない人が一ヶ月位で勉強を終えてしまうことが可能です。

簡単な問題こそ、計算速度が大事になってきます。計算速度に含まれるかもしれませんが、大事なのは「正しい公式の選び方」です。

こういう時こそ、落ち着いて、「書き始める前に選択肢をさらっと２０秒で思い浮かべる」習慣を付けましょう。

「あれ？簡単に見えるってことは、落ち着いてベストを探そう」
そう思えるようなら、大丈夫。簡単に見える問題は簡単です。(※広く捉えられる言葉や複雑な言葉で構成されている問題は、簡単に見えているだけなので注意。)

勉強のやる気が無くなってしまう大きな原因に「飽きる」があります。反射的に処理して、表にして、1分間でどんどんまとめていく習慣をつけましょう。

理解速度が上がりすぎて、勉強せずにはいられなくなりますよ！！　＾O＾

より詳しい説明がほしい方は、いつでもコメント下さい！また、解説して欲しい問題も、募集しています。

第１１回．特別授業－医学部物理解法（帝京大学2013物理大問3）

【タイトル】
〜それでも物理を選びませんか？〜

物理の効率的な勉強手順。「言葉からの反射」で、難関な医学部の問題を教科書の公式だけで反射的に解く

【前説】

今回は、今までのまとめをします。

【対象の学力層】
言葉からの反射を使って、医学部の入試問題を教科書に載っている単純な公式まで分解していきます！

今日から、医学部レベルの学力を「分単位！！」で身に着けていきましょう。

【物理の対策】
「特殊な計算が関わる理科の苦手克服」に入る前に、まず特殊計算について考えてみましょう。

ベストは何でしょう？

それは、「言葉からの反射」なんです

数学にしろ、英語にしろ、理科各科目にしろ、正しい勉強は決まっています。

まとめていきましょう。

【レベル１】
① 今まで帝京大学を扱ってきました。

② 物理を重視してきました。

③ 大事なのは、言葉からの反射でした。

④ 言うまでもなく、教科書に載っている公式だけで全て反射的に解けるようになってもらうことが目的です。

【レベル２】
1つずつ、掘り下げていきましょう！

① 帝京大学を扱ってきたのは、最も受験者数が多い医学部だからです。その理由として大きいのは、何と言っても受験日が多いこと(３回以上のチャンス！！)。それから、科目選択が幅広いことでしょう。

② その中で、物理はおすすめ科目です。帝京大学は、数学が難しく、物理が簡単です。英語・生物・化学は普通なので、この中から２科目選ぶと良いでしょう。

③ 帝京大学や物理という科目に限ったことでは有りません。言葉からの反射が最も大事なことです。人はどうしても、回りくどくなりがちです。言い訳したくなったり、色々なことが気になったり。そうではなく、言葉からの反射を使うことにより、何よりも早く解決に迎えるようにこだわりましょう。

④ ということは、言葉からの反射で公式に繋ぐことを何度も練習します。志望校の過去問を読み、言葉と公式を結びつけていく。いくつか可能性が考えられる場合は、予備校講師が書いた多くの本も、解説は回りくどいことが多いようです。言葉からの反射を一見長く見えても積み重ねていくことで、頭は高速処理され、結果として(a)広い視野で問題を見ること(b)多くの選択肢を考える事が出来るようになります。

【レベル３】
以上のことから物理の勉強法は、

① 公式をシンプルに理解する。(「物理１０１」は、教科書レベルだけシンプルにまとまっているのでおすすめです。)

② その公式を、問題文の専門用語から結びつける。実戦的に「言葉からの反射」を使いこなして行く。

いきなり過去問をやることは、難しく感じると思います。でも実は、それこそが一番早い勉強法なのです。だって、過去問が初見で解ければ受かるってことなのですから。

この勉強法を使えば、30時間で帝京大学医学部の物理が解ける全貌が、見えてくることでしょう。

もしくは、私に直接質問してください。

【終わりに】
医学部の物理ですら、九九しかできない人が一ヶ月位で勉強を終えてしまうことが可能です。

物理という一見難しく見える科目、食わず嫌いが最も多い科目。その科目の、最も効率的な学習法について、私ももっともっとこだわっていきます！！

勉強のやる気が無くなってしまう大きな原因に「飽きる」があります。反射的に処理して、表にして、1分間でどんどんまとめていく習慣をつけましょう。理解速度が上がりすぎて、勉強せずにはいられなくなりますよ！！　＾O＾

より詳しい説明がほしい方は、いつでもコメント下さい！また、解説して欲しい問題も、募集しています。

第１２回．特別授業－医学部数学解法（東海大学数学2013年第3問）

【タイトル】
〜図形問題、苦手ですか？〜

「言葉からの反射」で、難関な医学部の問題を教科書の公式だけで反射的に解く

【前説】

今回は、医学部受験の入門大学として人気な東海大学。その中でも最もメジャーな加もすべき科目、数学を例にとって説明します。

【門脇メソッド】
苦手な図形も、問題文が簡単なら大丈夫。「図からの反射」を使って、反射的に処理できますよ。

【対象の学力層】
(中級ランクまでしか受けない人は、「終わりに」の前から読んで下さい)

言葉からの反射を使って、医学部の入試問題を教科書に載っている単純な公式まで分解していきます！

今日から、医学部レベルの学力を「分単位！！」で身に着けていきましょう。

【数学の対策】
「言葉からの反射」に入る前に、今回は、数学の対策について説明しますね！

数学は、

知識、知識の関連性	少ない、多い
論理展開	大

と言えます。

こういう科目は、「言葉からの反射」と多岐に渡る可能性の比較が重要です。ただ、東海大学なら、センター試験程度で十分でしょう。

では、解く＆覚えていきましょう。

レベル１レベル２　では非常に単純化していきましょう＋言葉からの反射表を作っていきましょう。

ところで今回の問題は、図形問題なのに図が有りません。簡単な問題かも？と、問題選択の時に考えてみても良いかもしれません。 それでは、始めましょう。

【問題】

東海大学数学2013年第3問

△OABにおいてOA=5、AB=3(ﾙ-ﾄ)3、∠OAB=30∘とする。

(1) OBの長さはアである。また、△OABの面積はイである。
(2) cos∠AOB=ウである。よって、ベクトルOA→とOB→の内積OA→⋅OB→の値はエである。
(3) 点Oから辺ABに下ろした垂線と辺ABとの交点をPとする。このとき、APの長さは、ABの長さのオ倍である。さらに、点Bから辺OAへ下ろした垂線と直線OPとの交点をHとすると、OHの長さはOPの長さのカ倍である。BHの長さはキである。

△OABにおいてOA=5、AB=33、∠OAB=30∘とする。
とあるので、図を描きましょう。

図を描いてみると、余弦定理を使う図であることがわかります。

OB・・・余弦定理

（図に記入）

△OABの面積・・・面積公式

cos∠AOB・・・余弦定理

ベクトルOA→とOB→の内積・・・内積公式

「APの長さは、ABの長さのオ倍」

とあるので、ABを含む公式・・・ベクトルを使えない・・・レベル２（さらに論理展開）へ・・・それぞれ別の公式から繋ぐor計算して値で比べる・・・後者を選択・・・

AP：OAPの一辺・・・三角比

AB：○

「OHの長さはOPの長さのカ倍」

とあるので、OPを含む公式・・・ベクトルを使えない・・・レベル２（さらに論理展開）へ・・・それぞれ別の公式から繋ぐor計算して値で比べる・・・後者を選択・・・

OH：OPーPH・・・

OP、PH；下記、BPHの一辺・・・三角比

OP：OBPの一辺・・・三角比

BH・・・BPHの一辺・・・三角比

計算は割愛しますが、答は順番に、

(ﾙ-ﾄ)７、15(ﾙ-ﾄ)３/４、(ﾙ-ﾄ)7/14、5/2、5/6、2/5、(ﾙ-ﾄ)3

さて、今回は、図形の問題でした。

「言葉からの反射」はもちろん、「図からの反射」を使って解くことが大事です。焦らず、話の流れ通りに、言葉通りに図を描きましょう。また、並行して言葉からの反射を行いましょう。

帝京大学以上しか受けない人等のこの問題を簡単だと思った人は、今あなたがやっているレベルをこのように解いてみてください。きっとルールが見えてきて、今あなたがやっている問題でつまづくことが無くなるはずです。

決してこねくりまわすことなく、書きすぎることなく、かといって止まることもなく、「言葉からの反射」「図からの反射」で簡潔に考える修正をつけましょう。話が長くなると、自分が混乱しちゃいますよ？

【終わりに】
医学部の数学ですら、九九しかできない人が１ヶ月位で勉強を終えてしまうことが可能です。特に数学と言えども、東海大学は本当に簡単です。今後も、効率よく勉強して、はやくお医者さんになりましょう！

数学が得意でも、図形が苦手な人は多いです。でも、図を描いてみると、反射的に公式が浮かぶものが多いのです。

勉強のやる気が無くなってしまう大きな原因に「飽きる」があります。反射的に処理して、表にして、1分間でどんどんまとめていく習慣をつけましょう。理解速度が上がりすぎて、勉強せずにはいられなくなりますよ！！　＾O＾

より詳しい説明がほしい方は、いつでもコメント下さい！また、解説して欲しい問題も、募集しています。