2016年6月の記事

メディカルクオークグループの代表を務める門脇先生が数学と理科の特別授業を行います。

難易度の高い問題も簡単に解りやすく解説してくれます。

授業を通じて効率の良い学習法・解法を身につけていきましょう。

第１６回．特別授業－医学部数学解法（東海大学数学2013年第2問【2】前半）

【タイトル】
〜数列、その合理的な解き方２〜

「言葉からの反射」で、難関な医学部の問題を教科書の公式だけで反射的に解く

【前説】
今回は、医学部受験の入門大学として人気な東海大学。その中でも最もメジャーな加もすべき科目、数学を例にとって説明します。

【門脇メソッド】
「言葉からの反射」(問題はワンセットで覚える)
受験は、人生の縮図。 本番は必ず見たことがない形の問題が出ます。 導入、問題の区切れなどいろいろな罠にかからず、飽くまでも「言葉からの反射」を心がけましょう。そうすると・・・

【対象の学力層】
(上級～中級ランクまでしか受けない人は、「終わりに」の前から読んで下さい)

言葉からの反射を使って、医学部の入試問題を教科書に載っている単純な公式まで分解していきます！

今日から、医学部レベルの学力を「分単位！！」で身に着けていきましょう。

【数学の対策】
「言葉からの反射」に入る前に、今回は、数学の対策について説明しますね！

数学は、

知識、知識の関連性	少ない、多い
論理展開	大

と言えます。

こういう科目は、「言葉からの反射」と多岐に渡る可能性の比較が重要です。ただ、東海大学なら、センター試験程度で十分でしょう。

※【数列の対策】
あまり科目や分野を特別視したくは有りませんが、今回は泣く泣く。今回は、数列の問題です。

門脇メソッドのカリキュラムとしても、「言葉からの反射」「規則性を見つけたら表にする」（「薄い知識をミルフィーユ」も少々）

などを学ぶためにまずは関数・図形分野に着手しますが、数列は色々なコツがあるので、別にしてまとめて取り扱っています。

なお、

「レベル１レベル２　では非常に単純化していきましょう＋言葉からの反射表を作っていきましょう。」

は、紙面の関係で割愛しました。

では、解く＆覚えていきましょう。

【問題】

(２)(３)

エ、オ、カ

「聞かれてること＝」で考えると、α、βを考えたい。
α　β　 はこの式に書かれている

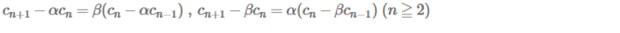
この式はこの漸化式から　α　β　が定まると書いてあるのでこの漸化式

を使う

先ほどの　 ｐ　 を代入してこの形

これは三項間漸化式なので その公式を使う
α　β　はこうなる

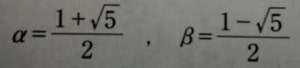
また三項間漸化式の 公式の続きから 　c　（n）　 はこうなる

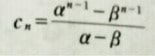
a　（n）　を 聞かれているので最初の式に代入する

その中の　ｃ　（n）　 は先ほど求まっていて　ｂ　（n）　は最初に戻るとこうなる

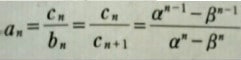
ク

極値を聞かれているので代入。

極限値の計算の手順どおり計算すると答えはこうなる

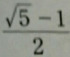
【コラム】
(２)(３)は、区切れ目を変えて解く問題だった。

括弧の 見た目に騙されて、つい先入観にとらわれてしまいがちだが、あくまで言葉からの反射。公式を覚えた通りに着手したい。

この場合3項間漸化式の解き方という一連の動作で出来上がっているので、着手を始めたら一連の動作の最後まで解けるはずである。

「言葉からの反射」を使い、手が止まることは最小限に抑えたい。これは、いつも通り。

また、いつも手が止まらずに解けるのに本番では解けない。こんなことが起きた場合、着眼点を変えてみよう。むやみに変えるのではない。

今回は、「区切りがいいところまで一気に解いちゃう」という自然な心理に従った。

普段から解説を読んだり予備校で聞いたりしてると思います。それは行き当たりばったりの解法であることが多いので、より合理的な手順を教師にも問うようにして下さい。それでもダメなら、私に質問を送ってくださいね！

帝京大学以上しか受けない人等のこの問題を簡単だと思った人は、今あなたがやっているレベルをこのように解いてみてください。

きっとルールが見えてきて、今あなたがやっている問題でつまずくことが無くなるはずです。

「参考書の解法はルールがない！なんでこの問題だけ変な解き方をするの？」といった意見をよく聞きます。

決してこねくりまわすことなく、書きすぎることなく、かといって止まることもなく、「言葉からの反射」「図からの反射」で簡潔に考える修正をつけましょう。話が長くなると、自分が混乱しちゃいますよ？

【終わりに】
医学部の数学ですら、九九しかできない人が１ヶ月位で勉強を終えてしまうことが可能です。特に数学と言えども、東海大学は本当に簡単です。今後も、効率よく勉強して、はやくお医者さんになりましょう！

「一旦後回しにして他の問題から少しずつ時間を集める」という、「元気玉」の発想。本番では、計算をいつもどおりやらないと時間が足りませんね。

勉強のやる気が無くなってしまう大きな原因に「飽きる」があります。反射的に処理して、表にして、1分間でどんどんまとめていく習慣をつけましょう。理解速度が上がりすぎて、勉強せずにはいられなくなりますよ！！　＾O＾

より詳しい説明がほしい方は、いつでもコメント下さい！また、解説して欲しい問題も、募集しています。

第１７回．特別授業－医学部物理解法（東海大学物理2013年第１問）

【タイトル】
〜「コレを使って解け」→「コレ以外のものは使わないか、途中式で消えるよ。」〜

「言葉からの反射」で、難関な医学部の問題を教科書の公式だけで反射的に解く

【前説】
今回は、医学部受験の入門大学として人気な東海大学。その中でも、物理を例にとって説明します。

【門脇メソッド】
「言葉からの反射」条件はむしろヒント

受験は、人生の縮図。飽くまでも「言葉からの反射」、制限はヒントとして考えることを心がけましょう。そうすると・・・

【対象の学力層】
(上級～中級ランクまでしか受けない人は、「終わりに」の前から読んで下さい)

言葉からの反射を使って、医学部の入試問題を教科書に載っている単純な公式まで分解していきます！

今日から、医学部レベルの学力を「分単位！！」で身に着けていきましょう。

【物理の対策】
「言葉からの反射」に入る前に、今回は、数学の対策について説明しますね！

数学は、

知識、知識の関連性	最少、多い
論理展開	中

と言えます。

こういう科目は、「言葉からの反射」が全てです。東海大学なら、平易な公式集か、そもそも教科書の裏表紙で十分でしょう。

レベル１レベル２　では非常に単純化していきましょう＋言葉からの反射表を作っていきましょう。

【問題】

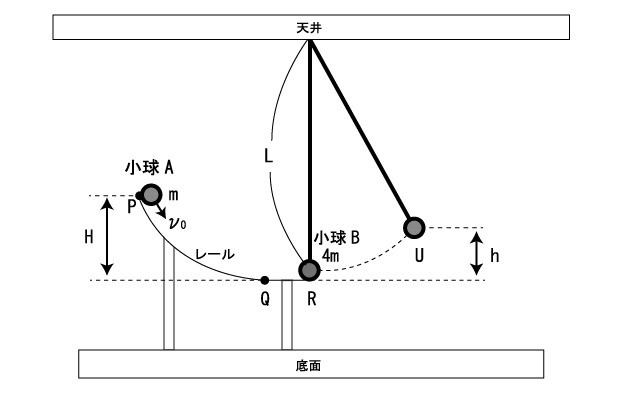
図のように、点Pから点Rに至るレールが支持棒により水平な底面から浮かせて固定されている。このレールは、最高点Pから点Qに至る曲線部と、点Qから点Rに至る水平部から成り、点Qで滑らかにつながっている。

レールの最高点Pは点Rよりも鉛直高さHだけ高い位置にある。

また、天井の点Tに一端が固定された長さL（L＞H）の伸び縮みしない軽い糸で鉛直に吊り下げられた小球Bが点Rに位置している。

ただし、小球Bは糸によってのみ支えられており、レールからの抗力は受けていない。いま、点Pから質量ｍの小球Aを初速ν₀でレールに沿って打ち出した。

小球Aはレールに沿って滑り降り、点Qを通過して点Rにおいて小球Bと正面衝突した。
小球Bの質量は４ｍであり、小球Aと小球Bのはねかえり係数は0.5である。

小球Aが小球Bに衝突した後、小球Aはレールに沿って跳ね返され、
小球Bは固定点Tを中心とする半径Lの円弧に沿った運動をして点Rよりも鉛直高さh（h＞L）だけ高い最高点Uに到達した。

レールの表面は滑らかで摩擦はなく、また空気抵抗もないとする。

重力加速度の大きさをｇとして、以下の各問に答えなさい。

なお、以下の各門においては、小球Aga初めて点Rに到達して小球Bと衝突する場合、およびその衝突による運動を考えるものとする。

また、小球Aと小球Bの運動は全てレールを含む鉛直面内で行われるものとする。

（１） 小球Aと小球Bの衝突直前の小球Aの速さをｇ、ｍ、H、ν₀の中から適切な記号を用いて求めなさい。

（２） 小球Aと小球Bの衝突直後の小球Bの速さをｇ、ｍ、H、ν₀の中から適切な記号を用いて求めなさい。

（３） 衝突後に小球Bが到達する高さをｇ、ｍ、H、ν₀の中から適切な記号を用いて求めなさい。

（４） 小球Aと小球Bの力学的エネルギーの和はこの衝突によってどれだけ減少したのか、ｇ、ｍ、H、ν₀の中から適切な記号を用いて求めなさい。

（５） 小球Aと初速ν₀が0のとき、衝突後に小球Bが到達する高さがLの１/20となるのはHがいくらのときか。Lを用いて求めなさい。

ふぅ、まずね、長すぎ、仮定！！
国公立志望者や充分な演習をこなしまくってる人はさておき、普通は前から忘れていっちゃいますよ！！

そこで、言葉からの反射を使ってシンプルにすると、

（１）
衝突→運動量保存則？→まだぶつかってないから違う
g,m,H,v0→力学的エネルギー保存則

（２）
衝突した→運動量保存則→

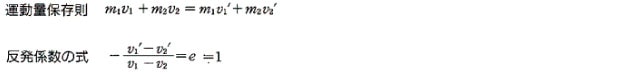
論理展開としては、

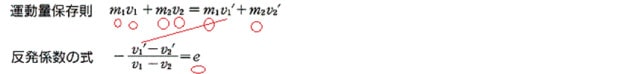
と考えて、　v2’　がわかる。

（３）
g,m,H,v0→力学的エネルギー保存則

（４）
減少：差→後ろー前
注意点：衝突直後：Bも高さ０

（５）
衝突後にBが到達する高さ：（３）→（３）に代入

レベル３としては、いつものように公式に代入して計算するだけです！

こんなにシンプルに出来ちゃいます。

普段から解説を読んだり予備校で聞いたりしてると思います。

それは行き当たりばったりの解法であることが多いので、より合理的な手順を教師にも問うようにして下さい。それでもダメなら、私に質問を送ってくださいね！

帝京大学以上しか受けない人等のこの問題を簡単だと思った人は、今あなたがやっているレベルをこのように解いてみてください。

きっとルールが見えてきて、今あなたがやっている問題でつまずくことが無くなるはずです。

「参考書の解法はルールがない！なんでこの問題だけ変な解き方をするの？」といった意見をよく聞きます。

決してこねくりまわすことなく、書きすぎることなく、かといって止まることもなく、「言葉からの反射」「図からの反射」で簡潔に考える修正をつけましょう。話が長くなると、自分が混乱しちゃいますよ？

【終わりに】
医学部の物理ですら、九九しかできない人が１ヶ月位で勉強を終えてしまうことが可能です。数学すら簡単な東海大学なので、物理は本当に簡単です。今後も、効率よく勉強して、はやくお医者さんになりましょう！

「言葉からの反射」を使って、出来る限りシンプルに考える習慣を付けましょう！

勉強のやる気が無くなってしまう大きな原因に「飽きる」があります。反射的に処理して、表にして、1分間でどんどんまとめていく習慣をつけましょう。

理解速度が上がりすぎて、勉強せずにはいられなくなりますよ！！　＾O＾

より詳しい説明がほしい方は、いつでもコメント下さい！また、解説して欲しい問題も、募集しています。

第１８回．特別授業－医学部数学解法（東海大学数学2012年第１問）

【タイトル】
〜時間との勝負は「元気玉」の発想〜

「言葉からの反射」で、難関な医学部の問題を教科書の公式だけで反射的に解く

【前説】
今回は、医学部受験の入門大学として人気な東海大学。その中でも最もメジャーな加もすべき科目、数学を例にとって説明します。

【門脇メソッド】
「一旦後回しにして他の問題から少しずつ時間を集める」という、「元気玉」の発想

受験は、人生の縮図。何より時間が大切です。「言葉からの反射」を使って反射的に処理して、時間を生み出しましょう。また、普段から自分の速度を把握しておきましょう。

【対象の学力層】
(上級～中級ランクまでしか受けない人は、「終わりに」の前から読んで下さい)

言葉からの反射を使って、医学部の入試問題を教科書に載っている単純な公式まで分解していきます！

今日から、医学部レベルの学力を「分単位！！」で身に着けていきましょう。

【数学の対策】
「言葉からの反射」に入る前に、今回は、数学の対策について説明しますね！

数学は、

知識、知識の関連性	少ない、多い
論理展開	大

と言えます。

こういう科目は、「言葉からの反射」が全てです。こういう科目は、「言葉からの反射」と多岐に渡る可能性の比較が重要です。ただ、東海大学なら、センター試験程度で十分でしょう。

では、解く＆覚えていきましょう。

【今回の問題に関して】
ところで今回の問題は、（１）のイだけ、少しややこしいですが、後はほぼ公式１発です。

また、「時間の元気玉」を使うわけですが、今回の問題は結果としてほぼ全てが簡単な小問です。他の難問に時間を分けてあげましょう。

「レベル１レベル２　では非常に単純化していきましょう＋言葉からの反射表を作っていきましょう

【問題】

(1)
ア
ベクトルの面積の公式→計算

イ
点の存在範囲の面積を聞かれている
点の存在範囲の公式：　a≦s+t≦b　に持っていく→計算
面積の公式　三角形ー三角形→計算

ウ　エ
因数定理→計算

オ
「全て異なる目」
確率の公式
一部：「全て異なる目」=順列の公式→計算
全体：重複順列の公式→計算

カ
和積の公式→計算

キ
公式が無い→公式を使う計算方法を考える
Cos２倍角が使える→２倍角の公式→計算

ク
公式が無い→公式を使う計算方法を考える
１　t　をかけて解の公式や解と係数の公式
2　２乗して真ん中に定数項を作る
(実は、一流高校受験では、2が公式として認知されている。)

【コラム】
医学部とは。

医学部とは、ミスが少ない人材を求める学部である。命を大切に扱うことを、科学的な発見(理学)やそれを実社会に応用させる(工学)ことよりも重視する学部である。

よって、高得点やそつくなこなす(小論文、面接)ことを求めてくる。

小問集合は、今回のように簡単なことが多い。しかし、他の問題も今回の問題のように、息を吐くように疑いなく処理できるまで、繰り返してほしい。

最終的な答えは、こうなる。

ア
√５
8√５
１３
-１７
５/９
-√2/ 2
４t/ 1-t2乗
5√12

さて、今回は最大速度で解く問題でした。

「一旦後回しにして他の問題から少しずつ時間を集める」という、「元気玉」の発想で臨むためにも、簡単なことに迷わず、高速で処理しましょう。

臨機応変、という言葉を悪用する人が多いように感じます。

状況に応じた「言葉からの反射」を徹底して叩き込み、思い付きではない裏付けのある処理をするよう心掛けて下さい。

帝京大学以上しか受けない人等のこの問題を簡単だと思った人は、今あなたがやっているレベルをこのように解いてみてください。きっとルールが見えてきて、今あなたがやっている問題でつまずくことが無くなるはずです。

「参考書の解法はルールがない！なんでこの問題だけ変な解き方をするの？」といった意見をよく聞きます。

決してこねくりまわすことなく、書きすぎることなく、かといって止まることもなく、「言葉からの反射」「図からの反射」で簡潔に考える修正をつけましょう。話が長くなると、自分が混乱しちゃいますよ？

【終わりに】
医学部の物理ですら、九九しかできない人が１ヶ月位で勉強を終えてしまうことが可能です。数学すら簡単な東海大学なので、物理は本当に簡単です。

今後も、効率よく勉強して、はやくお医者さんになりましょう！

「一旦後回しにして他の問題から少しずつ時間を集める」という、「元気玉」の発想。本番では、計算をいつもどおりやらないと時間が足りませんね。

勉強のやる気が無くなってしまう大きな原因に「飽きる」があります。

反射的に処理して、表にして、1分間でどんどんまとめていく習慣をつけましょう。理解速度が上がりすぎて、勉強せずにはいられなくなりますよ！！　＾O＾

より詳しい説明がほしい方は、いつでもコメント下さい！また、解説して欲しい問題も、募集しています。

第１９回．特別授業－医学部物理解法（東海大学物理2013年第２問）

【タイトル】
〜皆さん手を付けないでお馴染み、原子物理〜

「言葉からの反射」で、難関な医学部の問題を教科書の公式だけで反射的に解く

【前説】
今回は、医学部受験の入門大学として人気な東海大学。その中でも、物理を例にとって説明します。

【門脇メソッド】
「言葉からの反射」未修分野でも、閃ける

確かに原子物理をノータッチで受験に臨む人も多かったでしょう。でも、原子物理とはいえ、聞かれることはそれまでにやっていた分野で解けることも多いのです。とりあえず、言葉からの反射と簡単な公式であがいてみましょう

そうすると・・・

【対象の学力層】
(上級～中級ランクまでしか受けない人は、「終わりに」の前から読んで下さい)

言葉からの反射を使って、医学部の入試問題を教科書に載っている単純な公式まで分解していきます！

今日から、医学部レベルの学力を「分単位！！」で身に着けていきましょう。

【物理の対策】
「言葉からの反射」に入る前に、今回は、物理の対策について説明しますね！ 今日は物理なので、

知識、知識の関連性	最少、多い
論理展開	中

と言えます。

こういう科目は、「言葉からの反射」が全てです。東海大学なら、平易な公式集か、そもそも教科書の裏表紙で十分でしょう。

では、解く＆覚えていきましょう。

レベル１レベル２　では非常に単純化していきましょう＋言葉からの反射表を作っていきましょう。

【問題】

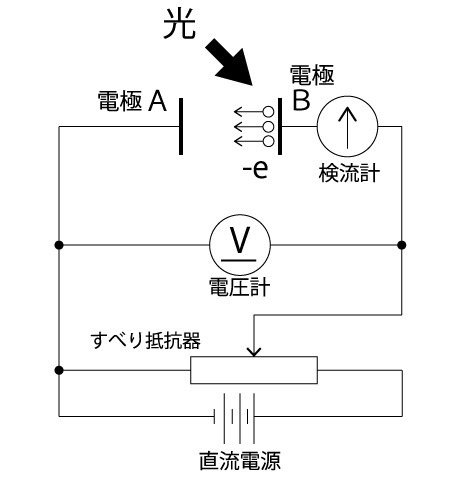
ある波長の光を金属電極に照射すると電極から電子が飛び出すことが知られている。

図の示すように、真空中に2枚の金属でできた電極Aと電極Bが平行に置かれている。

すべり抵抗器と直流電源を用いることにより電極A、B間の電圧は変化させることができるようになっている。

電子の質量をm、電荷を－e（e＞0）とし、電子に働く重力の影響、また、検流計の内部抵抗の影響は考えないものとして、以下の各問に答えなさい。

答えはそれぞれの解答群の中から最も適切なものを一つ選び、解答欄の記号にマークしなさい。

電極Bにある波長の光を照射したところ、初速ν₀で電子が電極Bを飛び出し検流計に電流が流れた。このとき、電圧計の指示値はＶ（Ｖ＞0）であった。

（1） 電極Ａ，Ｂ間の電場の向きと、電極Ｂあら飛び出した電子に働く静電気力の向きを求めなさい。

（2） 電極Ｂから飛び出した直後の電子の運動エネルギーを求めなさい。

（3） 電子が電極Ｂから電極Ａに到達するまでに静電気力がする仕事を求めなさい。

（4） 電子が電極Ａに到達する直前の速さを求めなさい。

電極Ｂにこの波長の光を照射し続けながら、電圧計の指示値がＶより増加するようにすべり抵抗器を操作すると、ある電圧になったとき電流が流れなくなった。

（5） 電流が流れなくなったときの電極Ａ，Ｂ間の電圧を求めなさい。

【解答群】

ふぅ、まずね、長すぎ、仮定！！

先週に引き続き長いから、東海大学の物理の傾向ですね、もうこれは。

国公立志望者や充分な演習をこなしまくってる人はさておき、普通は前から忘れていっちゃいますよ！！

そこで、言葉からの反射を使ってシンプルにすると、

(1)

電場の向き
電位の向き（or静電気力の向き：次の問題！！）
電圧計が正：V B >V A
BからA

静電気力の向き
（１）、電子：「―」
AからB

(2)
運動エネルギーの公式
1/2 mv^2
代入して計算

(3)
静電気力がする仕事の公式
W=qV
ｑ＝-e
代入して計算

(4)
速さ
運動エネルギー
保存則
1/2 mv1^2- 1/2 mv2^2 =⊿W
代入して計算

(5)
電流が流れない
電流：電子の移動
電子が移動しない
電子の速度＝０
（４）に代入して計算

レベル３としては、いつものように公式に代入して計算するだけです！

こんなにシンプルに出来ちゃいます。

普段から解説を読んだり予備校で聞いたりしてると思います。

それは行き当たりばったりの解法であることが多いので、より合理的な手順を教師にも問うようにして下さい。

それでもダメなら、私に質問を送ってくださいね！

帝京大学以上しか受けない人等のこの問題を簡単だと思った人は、今あなたがやっているレベルをこのように解いてみてください。

きっとルールが見えてきて、今あなたがやっている問題でつまずくことが無くなるはずです。

「参考書の解法はルールがない！なんでこの問題だけ変な解き方をするの？」といった意見をよく聞きます。

決してこねくりまわすことなく、書きすぎることなく、かといって止まることもなく、「言葉からの反射」「図からの反射」で簡潔に考える修正をつけましょう。話が長くなると、自分が混乱しちゃいますよ？

【終わりに】
医学部の物理ですら、九九しかできない人が１ヶ月位で勉強を終えてしまうことが可能です。数学すら簡単な東海大学なので、物理は本当に簡単です。

今後も、効率よく勉強して、はやくお医者さんになりましょう！

「言葉からの反射」を使って、出来る限りシンプルに考える習慣を付けましょう！

勉強のやる気が無くなってしまう大きな原因に「飽きる」があります。反射的に処理して、表にして、1分間でどんどんまとめていく習慣をつけましょう。

理解速度が上がりすぎて、勉強せずにはいられなくなりますよ！！　＾O＾

より詳しい説明がほしい方は、いつでもコメント下さい！また、解説して欲しい問題も、募集しています。