2016年2月の記事

メディカルクオークグループの代表を務める門脇先生が数学と理科の特別授業を行います。

難易度の高い問題も簡単に解りやすく解説してくれます。

授業を通じて効率の良い学習法・解法を身につけていきましょう。

第1回．特別授業－数学「データの分析」

新課程の試験範囲でつまづく人が多いようです。今回は、勉強法と解法、同時に教えちゃいましょう。

問題ごと覚えた方が効率がいいので、下記の2つの問題で全てを理解してしまいましょう。

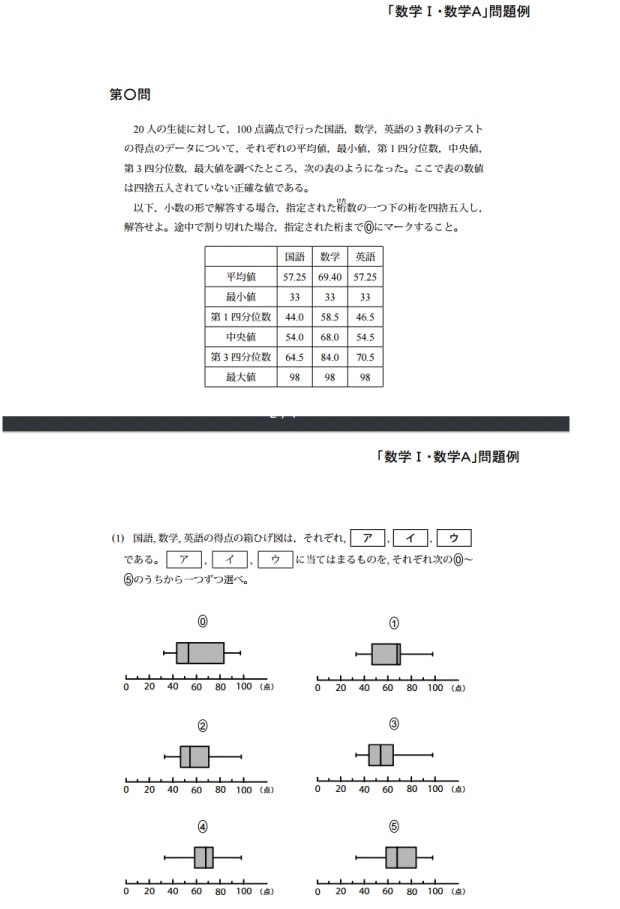
1つ目の問題。 「最小値」、「第１分位数」、「中央値」、「第３四分位数」、「最大値」。この、聞いたことない言葉を一気に覚えちゃおう。

では、最初の図を見てみよう。表の方、国語の欄を縦に見ると、最小値と最大値が書いてあるね。それを箱ひげ図の方でいうと、箱ひげの左端が33右端が98 真ん中が54になってるやつ。

これは3つとも、最小値と最大値の値が同じ。

中央値が54とか54.5 に見えるのは 0、 2、 3 番。

中央値が68なのは4、5、1番。

数学の方が簡単なので先にやろう。箱の右側が84.5に見えるのは 0と5番。だから 数学は5番。

国語と英語は四角(箱) の右側が70.5に見えるやつが 英語。 それは1番と2番 なので 英語 は2番。

国語は箱の右側が64.5に見えるやつなので３番。

ってことになります。これで、五個の言葉を覚えたね。

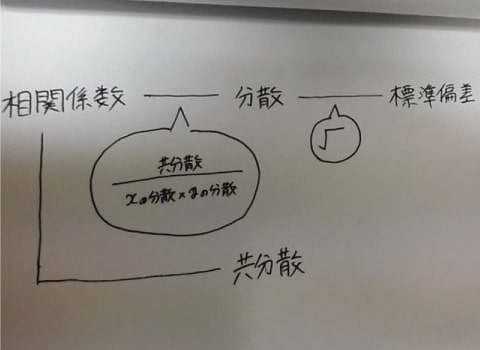
次に、他の言葉は２つ目の問題で覚えちゃおう。「 相関関数」、「分散」、「共分散」、「標準偏差」。

これは、この図みたいな関係があります。

では、問題で覚えよう。

この表で言えば平均値は、数学(以下、ｘ)の方は42、英語(以下、ｙ)の方は56。

次に、いよいよ分散と共分散。どっちの式でも使えるので まず値と平均値の差を計算しちゃおう。

この表で言えば、まず、隠れているA,Bを計算すると、Aが36、Bが50。だから、値から平均値を引くと、36-42、48-56、51-42、46-56、57-42、71-56、32-42、65-56、34-42、50-56となる。これを計算しちゃおう。

ここの引き算で出した答えを使います。

次に分散を求めます。ｘの分散は、36-42のところが「-6」。「-6」の二乗で、36。 その後も全部二乗していって、全部足すと506。この表は横に5個あるので これを5で割る。だから、ｘの分散は、101.2。yの分散も同じことをすると、ってなりそうだけど、ここで読解力。

コツ：読解力

次に行って共分散を求めます

「yの分散はxの分散と同じ」と書いてある。

さっき作った2つの数の差を、掛けて足します。 たとえば 一番左だったら、(-6)(-8)、9(-10)、これを足していくと、１４１。例によって、５で割る。だから、共分散は、28.2。

ちなみに この５で割るっていう作業は、具体的に共分散を求めなさいと書いてない限りやんなくてもいい。だって全部どうせ5で割るんだから。

５で割ったもの同士を割ると、どうせ消えるって話になって無駄だからね。今回は、何でも出来る生徒になって欲しいから、1つ1つ最後まで求めています。

相関関数は、分散÷共分散だから、0.28。

ちなみに、この問題で出てこなかったけど、標準偏差は分散のルートなので、10ちょっとってことになります。「ちょっと」というのがポイントで、実際に問題に出てくるときは、簡単な数字になるはず！

ということで、新課程で教師も含めてみんなビビっている、「データの分析」を授業しました。

第２回．特別授業－数学解法(帝京大学)

今回は、受験者数が最も多い医学部である帝京大学。その中でも最もメジャーな科目である、数学を例にとって説明します。

門脇メソッド

小問集合を使って、門脇メソッドの最も重要な方法である、言葉からの反射を覚えていきましょう。

対象の学力層

言葉からの反射を使って、医学部の入試問題を教科書に載っている単純な公式まで分解していきます！

今日から、医学部レベルの学力を分単位で身に着けていきましょう。

レベル１　では非常に単純化していきましょう

では、問題(fig1)を御覧下さい。

（１）「接線」と書いてあるので、「接線公式」。「囲まれた面積を求めよ」と言われているので「囲まれた面積を求める公式」

（２）「等差数列」と書いてあるので、「等差数列の公式」。次に、「等比数列」と書いてあるので、「等比数列の公式」。

（３）「同じ数字がいくつか書いてある」ので、「重複順列の公式」

ここまで読んでいただければ、（１）は本当に簡単にとける問題、（２）は簡単、（３）は少し対策が必要な問題ということが分かります。

∵（２）は言葉そのものが公式に繋がりますが、（３）は少し読み取る必要性があるからです。

レベル２

では（２）をより深く説明していきます

等差数列の公式につないで行けばいいので、真ん中の項が両端の項の平均値と考えればいいわけですが このままだとfig2のようになってしまって計算ができません。「底が違う」からです

なので、「底」という「言葉から反射」して「底の変換公式」を使います

レベル２＋今日のColumn

では次に（３）をより深く説明していきます

今回は、場合の数という受験生が最も苦手とする分野なので、Columnとしてとりあげて、レベル２の先を深く説明していきます。

場合の数は非常に苦手な人が多い分野です。例えば、理工学部に進む学生の中でも、文系の人に質問をされたときに、微積は得意だけど場合の数はにがてなんだぁと言っている人が多い分野であります。

場合の数は、中学校受験 高校受験 大学受験とすべての受験で登場するのですが、それでも苦手なままの人が多いです。

それは、読解力が非常に要求されて、公式の選び方が難しい分野だからです。ここでは、場合の数の基本的な考え方をこの問題とともに覚えてほしいと思います！

場合の数は基本的には2段階です。

まずパターンを出して、次にそのパターンが発生する場合について処理する という流れを取ります。

P（順列）とC(組み合わせ) の使い分けが非常に難しく、その点にも注意してみてください。

では、問題(fig1)を御覧下さい。

例えば、1 1 1 2 3 4 というのは、1が三回重複していて、後は一回ずつ という考え方をします。

同じ数が1個ずつ 2個ずつ 3個ずつなど同数の場合は、一度に処理ができます。

例えば、３個あれば6C3 5C3 などと処理できます　

1が3回町伏している部分と 1回ずつ ちょうふくしている部分に分けることが出来ますので 1の部分は6文字から一文字選ぶので6c1 234の分は午後5時から3文字 love-de5c3という考え方になります 理解を深めるために 他の例を出すと 1 1 1 2 2 3 という状況の場合 同じ個数 重複しているものがないので 6c15c1 4c1というふうに分けます

ここまでが 「場合の数の１段階目：パターンを出す」というところです。次に「2段階目」について考えてみましょう。

「重複している」場合は、「重複順列の公式」です。これは「言葉からの反射」ですが、使い方が分かってない人が多いです。

先ほどの「１１１の部分が ３回重複」しています 実は「234も１回重複」しているという考え方をすると非常に公式の理解が簡単になります。

また、分母の数と分子の数が同じになることでケアレスミス・数え間違いをなくすことができます！

3の階乗分の6の階乗とやりがちですが、3の階乗 * 1の階乗 * 1の階乗 * 1の階乗分の6の階乗という意識をで考える習慣をつけましょう。

全体としての 計算の方法はこの手順に乗っ取って表(fig3)にしておきましたので御覧下さい！

今回は小問集合だったので、「では、「聞かれていること＝」から始めます。「言葉からの反射」。 」「では、スライムにバラす。」「では、公式選び。」「では、公式。」「では、○×付け。」「では、×について考えましょう。」は登場しなかったようです。

終わりに
ということで今回は、門脇メソッドの最も重要な方法である、「「言葉からの反射」で、難関な医学部の問題を反射的に解く」を説明しました。

より詳しい説明がほしい方は、いつでもコメント下さい！また、解説して欲しい問題も、募集しています。

第３回．特別授業－物理解法(日本医科大学)

文で見ると難しく感じるかも。

まずは、サラッと全部読んでみて。全体像が掴めるから。

その後、一段落ずつ読んで行って。

１つずつは簡単ってことが分かるから。飽くまでも、スライムが合体してキングスライムになって強く感じるだけだよ＾＾

バラしてみたら、所詮1つ1つはタダのスライム。

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

第３回の今回は、物理を指導します(今後、数学、化学、生物、社会、国語など1人で全科目解説予定)。

ここを読んでいるみなさんは、日本医科大が丁度国公立も含めた医学部全体の大学の真ん中に当たると思うので、ここを中心に説明していきます。

今回は、2008年の日本医科大の物理大問1の(ア)

補足

こういう長い文のやつは別に、ここの前のリード文を読まないでとりあえず設問からいけばいいです。

わからない所を後で探していけばOK。じゃないと全部読んでも忘れちゃうから。”

では、「聞かれていること＝」から始めます。「言葉からの反射」。

周期

では、キングスライムをスライムにバラす。(キングスライムは一見強そうだけど、所詮はスライムがくっついただけ。スライム(教科書レベル)に分解すれば必ず解けるのです)

この周期というのは円筒上ぐるっと周る周期ということになるので、こういう周期の公式です。Ｂ～Ａまでの間はＡからその先で状況がわかれます。

Ａから左の状況は半径Xの単振り子と同じ。右の状況は半径２Xの単振り子と同じ。この状況が、単振り子だということが解る。

では、公式選び。

周期のパターンは沢山あるので、まあ後で出しましょう。そのうち、これは単振り子の周期です。一往復するから周期なので、ここ重要。

一往復一周の間、じゃあ左側どれぐらいかっていうと、上がって下がってきて、通過して戻ってくるまでのが入ってないので、左半分しかないという感覚になるから１/２、右側も同様に上がって下がって、本当は一回通過して戻ってきて、

では、公式。

T(一周)=２π√l/g

では、○×付け。

２πは、この問題は一周じゃないので×。１は、分からないので、×。ｇは分かってる(定数)ので○。

では、×について考えましょう。

何周か。１って何か。

「聞かれていること＝」

言葉からの反射。

簡単な方から行くと、 Aの左側は半径X、右側は半径２Xということになります。だから、１(左)＝ｘ，１(右)＝２ｘ。

“点Aを通過する周期。普通の完全な所だったら、投げて行って帰ってきて一往復して。一往復というのが重要です。一周して戻ってくるのが周期。

今回は、Aの左側が半周なので、θ（左）＝π。Aの右側が半周なので、θ（右）＝π。”

代入すると、π√x/g＋π√2x/g

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

【今日のコラム】

ではここで 物理の勉強法。

解説を読み始めた時に上から読んでいく習性がみんなあると思うんだけど、解説は下から読んだ方がいいよ。

あと、接続詞の関係とかにちゃんと線を引っ張って、話の区切りを明確にして行きましょう。

今回の問題で言うと、ある解説には、点Aからずれた点で受ける力は・・・っていう話から始まってるんだ。

でも本当は聞かれていることは周期なので、あくまでも周期の問題についての方から考えていけばいい。「周期」に絡む物は、 「回転角度」と「１」と「g」。

ｌというのは 振り子の半径がどれくらいかという事。gは一般的な定数なので考える必要がない。だから角度がいくつかと、ｌがいくつかということを考えていけばいいという問題でした。

普段は（僕が解説している問題以外も勉強する場合は）、ちゃんと解説を読むことになると思います。解説を読むときは必ず、逆から呼んでいって綺麗に分けていく。

それで、その公式に、知らないことを代入していく。知らないことは問題文中から読み取れるわけですが、理解しながら解説を読むようにしてください。

頭から解説を読んでいくと、なんでこういう風に解説が書かれているのか分からない！ってなるけど、後ろから読んで行けば なんでそこを解説しているか分かると思います。